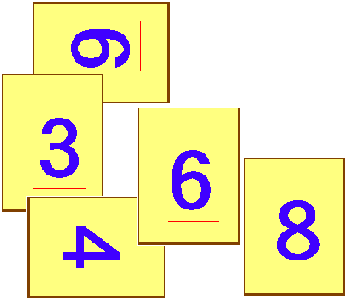
左図のように「３」と「４」と「６」と「８」と「９」の５枚のカードがあります。 　今、この５枚のカードから、４枚のカードを選んで並べて、４ケタの数字を作ります。 　このようにして作った数字全部の平均はいくらになるでしょうか。

＜答え　６６６６＞　　　　　 　　　　　　　　　　　

＜かつひこ　さん、tommyさん、まおさん、老眼鏡さん　ｔｅｋｉさん、CRYING DOLPHINさん他多数から頂きました＞

どの数字もどの桁の時にも同じ確率で選ばれるので
「（３＋４＋６＋８＋９）÷５＝６」となります。

＜ nother　さん＞

(3+4+6+8+9)*24*1111/120 としました。

＜ キヨタカ　さん＞
 まず５枚のカードから４枚のカードを選んで４桁の数字は、順列の公式
より、5Ｐ4＝１２０．よって１２０通り考えられる。
　次にこの4桁の数字の最小値は３４６８で最大値は９８６４になりそ
の合計は１３３３２になる。また、２番目に小さい数と２番目に大きい
数の合計も１３３２になる。以上のことから、１３３３２は全部で６０
個あるので、１３３３２×６０÷１２０＝６６６６

＜高橋　　さん＞ 
ずるい方法では、例えば3468と9854の平均が6666というように
ある数とその数の中の３を９に、４を８に、８を４に、９を３に
変えた数をペアにしていくと、重複なく、必ずペアがあり、
その平均が6666になりますから全体の平均も6666になります。

つぎにちょっとずるい方法は
各位の数の平均は、(3+4+6+8+9)/5=6なので6666になります。
というのは、
１の位が3,4,6,8,9になるのはそれぞれ６通りづつありますから
平均は正確に書くと(3+4+6+8+9)*6/(5*6)=6になります。
10の位,100の位,1000の位も同じだからです。

＜浜田　さん＞
エクセルのマクロです．

Option Explicit
Sub Macro1()
    Dim a(5) As Integer
    Cells(1, 1).Value = 3
    Cells(1, 2).Value = 4
    Cells(1, 3).Value = 6
    Cells(1, 4).Value = 8
    Cells(1, 5).Value = 9
    Cells(2, 1).Value = 0
    Cells(2, 2).Value = 0
    Cells(2, 3).Value = "=A2/B2"
    Range("C2").Select
    Call check(1, a())
End Sub
Sub check(ByVal n As Integer, ByRef a() As Integer)
    Dim wa As Long
    Dim j As Integer
    If n < 5 Then
      a(n) = 1
      While a(n) <= 5
        If dame(n, a()) = 0 Then
          Call check(n + 1, a())
        End If
        a(n) = a(n) + 1
      Wend
    Else
      a(5) = 5
      For j = 1 To 4
        a(5) = a(5) + j - a(j)
      Next j
      wa = Cells(1, a(1)).Value
      For j = 2 To 5
        wa = 10 * wa + Cells(1, a(j)).Value
      Next j
      Cells(2, 1).Value = Cells(2, 1).Value + wa
      Cells(2, 2).Value = Cells(2, 2).Value + 1
    End If
End Sub
Private Function dame(ByVal n As Integer, ByRef a() As Integer)
    Dim j As Integer
    dame = 0
    j = 1
    While dame = 0 And j < n
      dame = -(a(j) = a(n))
      j = j + 1
    Wend
End Function

＜Ｆuse　さん＞
最大から下りてくると、
9864,9863,9846,9843,9836,9834,9684,9683,,.....が並
び、
最小から上ると、　　　
3468,3469,3486,3489,3496,3498,3648,3649,.......が
並ぶ。

9864,3468の平均をとると、6666
9863,3469の平均をとると、6666
となり、すべて6666の平均が得られると予想されるの
で、6666としました。


＜BossF　ミミズクはくず耳　さん＞
各桁には各々の数字が同数表れるのは対称性より明らか
さて「３」と「４」と「６」と「８」と「９」の平均は６
よって求める平均は　６６６６…答

東京出版のHP内にある数算王神社の算額第18問
http://www.tokyo-shuppan.co.jp/susanowo/2001_018/index.html
とにてますね(^o^)

＜鈴木　さん＞
全ての組み合わせ、５×４×３×２＝１２０通り
千の桁が３の時の組み合わせ、４×３×２＝２４通り
千の桁が、その他の場合も各々２４通り
千の桁だけの合計を考えると、各々の数字が２４個づつあるので
２４×（３＋４＋６＋８＋９）×１０００＝７２００００
同様に百の桁　　２４×（３＋４＋６＋８＋９）×１００＝７２０００
同様に十の桁　　２４×（３＋４＋６＋８＋９）×１０＝７２００
同様に一の桁　　２４×（３＋４＋６＋８＋９）×１＝７２０
よって、全部の合計は、７２００００＋７２０００＋７２００＋７２０＝７９９９２０
平均は、７９９９２０÷１２０＝６６６６

＜巷の夢　さん＞
 数字の組み合わせが５通り、４個の数字の並べ方が２４通り、即ち、１２０通りの
４桁の数字ができる。そして、各々の文字は各桁とも２４回でるので−−−。

たくさんの回答有り難うございました。