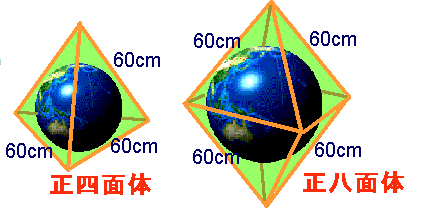
丂嵍偺恾偺傛偆偵丄堦曈偺挿偝偑俇侽們倣偺惓巐柺懱偲惓敧柺懱偺儌僯儏儊儞僩偑偁傝傑偡丅
丂偙偺拞偵丄偳偺柺偵傕愙偡傞傛偆偵抧媴媀偑擖偭偰偄傑偡丅
丂偙偙偱栤戣偱偡丅
丂惓敧柺懱偵擖偭偰偄傞抧媴媀偺敿宎偼丄惓巐柺懱偺抧媴媀偺敿宎偺壗攞偵側傞偱偟傚偆偐丅
丂
丂

|
丂 丂 |
摎偊偼俀攞偱偡丅
亙儈儈僘僋偼偔偢帹偝傫偺夝摎亜
丂曈偺挿偝偑60cm偺惓係柺懱偺奺柺枅偵丄奺曈偺拞揰傪寢傫偱惓嶰妏宍傪偮偔傞偲丄曈偺挿偝偑30cm偺惓俉柺懱偑偱偒傑偡丅
丂偙偺惓俉柺懱偺係柺偼丄尦偺惓係柺懱偲摨偠偱丄摨偠媴乮抧媴媀乯偵撪愙偟傑偡丅
偟偨偑偭偰丄曈偺挿偝偑60cm偺惓俉柺懱偵撪愙偡傞媴偺敿宎偼丄曈偺挿偝偑30cm偺惓俉柺懱偵撪愙偡傞媴偺敿宎偺2攞偼柧傜偐側偺偱丄曈偺挿偝偑60cm偺惓係柺懱偵撪愙偡傞媴偺敿宎偺俀攞偲傢偐傝傑偡丅
亙桳柍憡惗偝傫偺夝摎亜
堦曈傪a偲偟偰丄掙柺偺惓嶰妏宍偺柺愊傪俽丄掙柺偵捀揰偐傜
壓傠偟偨悅慄偺挿偝傪倛偲偡傞偲丄
懱愊亖1/3*俽*倛亖4*乮1/3*倰*俽乯
傪梡偄偰倰傪寁嶼偡傞偲偙傠傪丄3攞偲偟偰偟傑偄傑偟偨丅
倰亖a/sqr(24)偱丄惓敧柺懱偵撪愙偡傞媴偺敿宎R=a/sqr(6)側
偺偱丄R/r=2
摎偊偼俀偱偡丅
亙 崅嫶丂摴峀偝傫偺夝摎亜
惓巐柺懱偺媴偺敿宎
丂惓巐柺懱傪傂偲偮偺曈偲丄偦偺曈偲偹偠傟偺埵抲偵偁傞曈偺拞揰傪捠傞暯柺偱愗偭偨偲偒偺抐柺傪峫偊傑偡丅
偙偺抐柺偱丄AB=60,AM=BM=30併3偲偡傞偲BC:CM=2:1偲側傞
BM忋偺揰傪C,AD:DM=2:1偲側傞AM忋偺揰傪D偲偡傞偲AC偲BM偑悅捈乮惓4柺懱偺崅偝乯AM偲BD偼悅捈乮惓4柺懱偺崅偝乯偲側偭偰偍傝丄AC偲BD偺岎揰傪H偲偡傞偲丄棫懱偺懳徧惈偐傜HC偑媴偺敿宎偱偁傞偙偲偑傢偐傝傑偡丅
C偐傜AM偵悅慄傪壓傠偟懌傪E偲偡傞偲丄
BD偲CE偑暯峴側偺偱ME:ED=MC:CB=1:2
偙傟偲MD:DA=1:2偐傜AD:DE:EM=6:2:1
HD偲CE偑暯峴側偺偱丄AH:HC=AD:DE=6:2=3:1
傛偭偰HC偼AC偺1/4偱偁傞偙偲偑傢偐傝傑偡丅
乮懱愊傪棙梡偟偨曽朄偼慜偵憲偭偨偺偱暿側曽朄偱徹柧
偟偰傒傑偟偨乯
BC=30併3亊2/3=20併3
AC^2=AB^2-BC^2=3600-1200=2400丂AC=20併6
HC=1/4AC=1/4亊20併6=5併6
惓8柺懱偺媴
偙偪傜傕懱愊偱偩偝側偄偱傗傝傑偡丅
岦偐偄崌偆俀偮偺捀揰偲丄2偮偺曈偺拞揰傪捠傞暯柺偱丄偙偺棫懱傪
俀偮偵愗傝傑偡丅乮嵍塃懳徧偵側傞傛偆偵乯
偦偺抐柺傪偝傜偵懳妏慄偱係摍暘偡傞偲丄幬曈偑30併3,
傂偲偮偺曈偑30偺捈妏嶰妏宍偑偱偒丄媴偺敿宎偼丄偙偺捈妏嶰妏宍偺
幬曈傪掙曈偲偟偨偲偒偺崅偝偱偁傞偙偲偑傢偐傝傑偡丅
捈妏嶰妏宍偺傕偆傂偲偮偺曈偺挿偝偼丄60cm偺惓曽宍偺懳妏慄偺
1/2偐傜30併2乮嶰暯曽偐傜偱傕偱傑偡偑...乯
柺愊偺幃丂1/2亊30亊30併2=1/2亊30併3亊倛丂偐傜
倛=10併6
傛偭偰1:2偲側傝傑偡丅
亙倲倕倠倝偝傫偺夝摎亜
嘆丂惓巐柺懱偺撪愙媴偺敿宎
丂丂幬曈俁侽併俁丄掙曈侾侽併俁偺捈妏嶰妏宍偺崅偝偼丄
丂嶰暯曽偺掕棟傛傝丄俀侽併俇丂偲側傝傑偡丅
丂丂偙偺嶰妏宍偵偍偄偰丄幬曈偲掙曈偐傜摍嫍棧偵偁傞
丂曈忋偺揰偐傜偺嫍棧偼丄嶰妏宍偺柺愊偐傜俆併俇偲
丂側傝傑偡丅乮徻偟偄愢柧偼丄恾傪昤偐側偄偲擄偟偄偱偡偑乯
嘇丂惓敧柺懱偺撪愙媴偺敿宎
丂丂撪愙媴偺拞怱偑惓敧柺懱傪悈暯偵愗抐偟偨惓曽宍偺
丂柺忋偺懳妏慄偺岎揰偵偁傞偺偼柧傜偐偱偡丅
丂丂傛偭偰丄偦偺敿宎偼丄幬曈俁侽併俁丄掙曈俁侽偺捈妏嶰
丂妏宍偺柺愊傪幬曈偺挿偝偱妱偭偨傕偺偲側傝傑偡丅
丂丂廬偭偰丄撪愙媴偺敿宎偼丄侾侽併俇偲側傝傑偡丅
亙岼偺柌偝傫偺夝摎亜
惓巐柺懱偼敿宎偐傜丄惓敧柺懱偼暯柺恾偵偟偰柺愊偐傜
奺乆偺敿宎傪寁嶼偟傑偟偨丅
亙CRYING DOLPHIN偝傫偺夝摎亜
栤戣恾偵偁傞惓巐柺懱傪係屄丄惓敧柺懱傪侾屄傪偆傑偔愊傒廳偹傞偲丄侾曈偑侾俀侽cm偺惓巐柺懱偑姰惉偟傑偡丅
偙偺偲偒丄傕偲偺惓敧柺懱偺奺柺偵愙偡傞媴偼丄侾曈偑侾俀侽cm偺惓巐柺懱偺奺柺偵傕愙偟偰偄傑偡丅
傛偭偰丄侾曈偑侾俀侽cm偺惓巐柺懱偲侾曈偑俇侽cm偺惓巐柺懱偺奺柺偵愙偡傞媴偺敿宎傪斾傋傟偽乧乧惓巐柺懱偺憡帡斾偑偦偺傑傑媴偺敿宎斾偵側傝傑偡丅