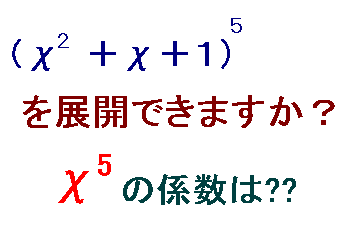
今回は、多項式を展開する問題です。
きっと、この式(X2+X+1)5 を展開すると、項の数は全部で、11個になると思います。
ここで問題です。
X5 の係数はいくらになるでしょうか。
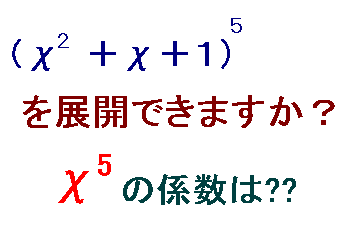 |
今回は、多項式を展開する問題です。 ここで問題です。
|
答えは、51でした。
<正解者一覧表>
| 正解者順位 | name | メール到着日時 | 備 考 |
| 1 | Michael さん | 2002/5/1 0:20 | |
| 2 | モルモット増殖中 さん | 2002/5/1 0:25 | モルモット王国 |
| 3 | ミミズクはくず耳 さん | 2002/5/1 0:30 | |
| 4 | なにわ さん | 2002/5/1 0:32 | 西宮市 |
| 5 | Banyanyan さん | 2002/5/1 0:58 | 京都府 |
| 6 | モルモット大臣 さん | 2002/5/1 3:19 | モルモット王国 |
| 7 | 信三 さん | 2002/5/1 3:27 | シリコンバレーの住人 |
| 8 | 有無相生 さん | 2002/5/1 8:47 | 神奈川県、会社員 |
| 9 | QPer さん | 2002/5/1 9:11 | |
| 10 | 巷の夢 さん | 2002/5/1 12:51 | 宮城県 |
| 11 | miya さん | 2002/5/1 16:48 | 熊本 |
| 12 | teki さん | 2002/5/1 18:00 | |
| 13 | 高橋 道広 さん | 2002/5/1 18:18 | 北の隠れ家 |
| 14 | BossF さん | 2002/5/1 22:20 | |
| 15 | N.Nishi さん | 2002/5/1 22:58 | 大阪府:中学教諭 |
| 16 | BEAN さん | 2002/5/2 0:08 | |
| 17 | 老眼鏡 さん | 2002/5/2 21:59 | 福岡ダイエー ファン |
| 18 | ISAMU さん | 2002/5/2 22:57 | 三重県 |
| 19 | ふじさきたつみ さん | 2002/5/3 10:37 | 北海道 |
| 20 | 暇な人間 さん | 2002/5/3 15:32 | |
| 21 | 岡田 さん | 2002/5/4 1:47 | 鳥取県出身 |
| 22 | 理一郎坊ちゃん さん | 2002/5/4 18:25 | 山口市湯田 |
| 23 | Parpunte さん | 2002/5/5 23:12 | 市川市のリーマン |
| 24 | まお さん | 2002/5/7 0:28 | 福井県 |
| 25 | 安楽克嘉 さん | 2002/5/7 9:01 | 宮崎県小林市 |
| 26 | あつしぃ さん | 2002/5/8 16:17 | 会社員 |
| 27 | 計算鑑定人 さん | 2002/5/9 7:45 | |
| 28 | aho さん | 2002/5/10 23:55 | 熊本 |
| 29 | LION さん | 2002/5/12 12:11 | 東京都 |
| 30 | テモ さん | 2002/5/14 23:47 | 広島市佐伯区美鈴が丘 |
| 31 | ルーキー さん | 2002/5/20 5:06 | 高校1年生 |
| 32 | 浜田 明巳 さん | 2002/5/24 14:55 | |
<ミミズクはくず耳 さん>
2項展開よりちょっと面倒ですね。
111
*111
**111
−−−−−−
12321
*12321
**12321
−−−−−−
1367631
*1367631
**1367631
−−−−−−−−−−−−
1,4,10,16,19,16,10,4,1
*1,4,10,16,19,16,10,4,1
**1,4,10,16,19,16,10,4,1
−−−−−−−−−−−−
1,5,15,30,45,51,45,30,15,5,1
<なにわ さんより>
こんなのがありました。
http://www.research.att.com/~njas/sequences/
Sequence:
3,16,51,126,266,504,882,1452,2277,3432,5005,7098,9828,13328,
17748,23256,30039,38304,48279,60214,74382,91080,110630,
133380,159705,190008,224721,264306,309256,360096,417384,
481712,553707,634032,723387,822510
Name: Coefficient of x^5 in expansion of
(1+x+x^2)^n
<モルモット大臣 さんより>
X^5はX^2×X^2とX、X^2とX×X×X,X×X×X×X×Xの組み合わせであり
5C2×3C1+5C1×4C3+5C5=51
<有無相生 さんより>
[x(x+1)+1]**5=x**5*(x+1)**5+5*x**4*(x+1)**4+10*x**3*(x+1)**3+10*x**2*(x+1)**2+....
x**5の係数は、第1項から1、第2項から20、第3項から30で計51.
<miya さんより>
(x^2+x+1)^5の一般項は
(5!/p!q!r!)・(x^2)^p・x^q・1^r
=(5!/p!q!r!)・x^2p+q・1^r
よって
2p+q=5、p+q+r=5
p、q、rの組は
(0,5,0)、(1,3,1)、(2,1,2)
(5!/5!)+(5!/1!3!1!)+(5!/2!1!2!)
=1+20+30=51
n=5でそんなに大きくないので実際に手計算でも
51という解はそんなに時間かからずに求めることもできました
< BossF さんより>
[略解] x5=(x2)2x(x1)1x(1)2 … 5!/(2!x2!)=30 =(x2)1x(x1)3x(1)1 … 5!/3!=20
=(x2)0x(x2)5x(1)0 … 1
よって 51…答
<N.Nishi さんより>
組み合わせで考えました。(間違ってたりして)
与式をχの次数だけで考えると(2,1,0)(2,1,0)(2,1,0)(2,1,0)
(2,1,0)となっていて、更に( )内の項の係数がすべて1というのがミ
ソ。
よってχの5乗の係数は全ての( )から「11111」(1を5つ)か
「01112」(0,2を1つずつ、1を3つ)「00122」(0,2を2つずつ、1を
1つ)をかけたものを考えればよい。全て係数が1なので何通りか数え
る。
「11111」で1通り
「01112」で20通り
「00122」で30通り
あわせて51通りなので
係数は51
<ふじさきたつみ さん>
二項定理をつかいました。
(x^2)^p*x^q*1^r=x^5とすると
(p、q、r)=(0,5,0)
(p、q、r)=(1,3,1)
(p、q、r)=(2、1,2)の3つがあって、
それぞれの係数は 5!/p!*q!*r!に代入して、1,20、30
だから、求める係数は、51となる。
<岡田 さん より>
x^2+x=Mとして(M+1)^5を二項定理でとく
M^5+5M^4+10M^3+10M^2+5M+1
Mをもどす
x^10+5x^9+15x^8+30x^7+45x^6+51x^5+45x^4+30x^3+15x^2+5x+1
よってx^2の係数は51
<あつしぃ さんより>
[解]
x^5 の係数は、
(x)*(x)*(x)*(x)*(x) の係数 ---- (A)
(x^2)*(x)*(x)*(x)*(1) の係数 ---- (B)
(x^2)*(x^2)*(x)*(1)*(1) の係数 ---- (C)
上記の係数を足せば良い。
(A) の係数は、5!/5!
= 1
(B) の係数は、5!/(1!・3!・1!) = 20
(C) の係数は、5!/(2!・2!・1!) = 30
[! は、階乗]
∴ x^5の係数は、 51
<LION さんより>
x^5 = (x^2)^2*x = (x^2)*(x^3) = x^5であるので、各々の係数を計算して足し算しました。
(30 + 20 + 1 = 51)
<浜田 明巳 さんより>
展開式
x^10+5x^9+15x^8+30x^7+45x^6+51x^5+45x^4+30x^3+15x^2+5x+1
x^5の係数
51
下記のUBASICのプログラムで解いてしまいました.ありきたりの解答ですみません.
10 'asave "m0205.ub"
20 print (_X^2+_X+1)^5
30 print ((_X^2+_X+1)^5\_X^5)@_X
40 end