「今月の問題」　第３５回　（平成１４年８月）

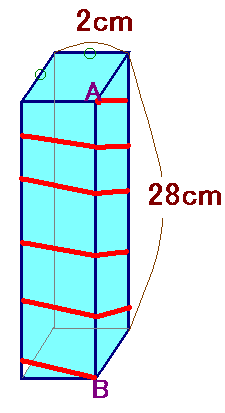
　左図を見てください。
　底面は２ｃｍの正方形で、高さが２８ｃｍの正四角柱があります。

　この正四角柱の一辺の両端点Aから点Bまで、１００ｃｍの赤いひもでまいてていきます。

　ここで問題です。

　赤いひもを点Aから点Bまで最短距離でまいていくと、何回まくことになるでしょうか。

　

＜正解者一覧表＞　　　　　 　　　　　　　　　　　
正解者順位 　　　　ｎａｍｅ　　　 　　メール到着日時　　 　　備　考　　
　１ 高田修成(修徳学院)　さん2002/8/1　0:10兵庫県
　２信三　さん2002/8/1　0:15シリコンバレーの住人
　３ maruhagedon　さん2002/8/1　0:18　
　４Banyanyan　さん2002/8/1　0:19京都府
　５Non　さん2002/8/1　0:23　
　６BEAN　さん2002/8/1　0:37　
　７ponta55555　さん2002/8/1　0:39　
　８Michael　さん2002/8/1　0:40　
　９POPPY　さん2002/8/1　0:53　
１０Nの悲劇　さん2002/8/1　1:00兵庫県・くそ忙しい塾講師
１１N.Nishi　さん2002/8/1　1:26大阪府：中学教諭
１２ステップ　ばい　ステップ　さん2002/8/1　2:24　
１３モルモット増殖中　さん2002/8/1　8:34モルモット共和国
１４理一郎坊ちゃん　さん2002/8/1　11:49山口市湯田
１５老眼鏡　さん2002/8/1　11:50今年はあきらめのダイエーファン
１６BB　さん2002/8/1　13:03東京都　事務系会社員３４歳
１７岡田　さん2002/8/1　17:48鳥取県出身　中３
１８モルモット大臣　さん2002/8/1　18:48モルモット王国
１９ミミズクはくず耳　さん2002/8/1　22:02神奈川県横浜市
２０なにわ　さん2002/8/2　1:08西宮市
２１ まお　さん2002/8/2　10:56福井県
２２村田　さん2002/8/2　19:19大阪市中央区　　歳：５３
２３巷の夢　さん2002/8/2　20:53宮城県
２４miya　さん2002/8/2　20:58熊本県
２５ なか　さん2002/8/3　6:44北海道
２６デジタラ〜　さん2002/8/3　10:13中２
２７ISAMU　さん2002/8/3　13:41三重県
２８ BossF　さん2002/8/3　15:19　
２９ 有無相生　さん2002/8/4　11:48神奈川県、会社員
３０スモークマン　さん2002/8/4　17:21ボケを怖がってるJijy
３１ 高橋　道広　さん2002/8/5　12:48北の隠れ家
３２ふじさきたつみ　さん2002/8/5　17:14北海道
３３teki　さん2002/8/6　13:07　
３４ CRYING DOLPHIN　さん2002/8/7　23:29高知市（推定）
３５yuki　さん2002/8/8　1:28奈良県
３６dr.m　さん2002/8/12　9:25阪神間の田舎者
３７圭太　さん2002/8/15　7:25　
３８kenkichi　さん2002/8/16　9:29　
３９テモ　さん2002/8/19　12:55広島市佐伯区美鈴が丘
４０浜田明巳　さん2002/8/22　8:19　
４１あああああ　さん2002/8/22　10:33　
４２ハリーポッチャリー　さん2002/8/22　10:40中学教師
４３おーちゃん　さん2002/8/27　7:06群馬県
４４吉見の沢北　さん2002/8/28　17:45山口県下関市高等学校１年

答えは、１２回です。

皆さんからの解答の一部を紹介させてもらいます。

＜N.Nishi　さんより＞
 単純に計算すれば13回も巻けませんでした(^^;
（１００÷８）
で、三平方の定理を使った二次不等式で丁度12回と。

＜ステップ　ばい　ステップ　さんより＞
１巻きで上る高さをｘｃｍとします。このとき（２８/ｘ〕回が求める
答えになります。
展開図を横に（２８/ｘ）枚つなげた長方形の対角線がＡからＢへの最
短経路です。この長さが１００ｃｍなので、
√(x^2＋８^2）×（２８/ｘ）＝１００。よってｘ＝７/３．
２８÷（７/３）＝１２．
こたえ　１２回。

＜BB　さんより＞
何重にもなった四角柱の展開図をイメージして
縦：２８、横：８ａ（ａは巻きつけた回数）、辺：１００とし
三平方の定理より、
28^2+(8a)^2=100^2
これを解くとa=12となります。

※なお、村田さんと浜田明巳さんからは、展開図を丁寧に書かれたjpeg図と解き方の説明を送っていただきました。
感謝！

＜有無相生　さん、高橋　さん、ふじさきさん　CRYING DOLPHINさん、yukiさん、圭太さん、おーちゃんさん　他多数の方から頂きました＞
 直角三角形の斜辺100ｃｍで他の一辺が28ｃｍのとき、もう一辺の長さ
は96ｃｍとなり、これを一周分8ｃｍで割ると12周となる。

　

また、高橋さんからはピタゴラス数について教えて頂きました。
ピタゴラス数
a=m^2-n^2　b=m^2+n^2　c=2mnのmとnに任意の数を入れると3辺がずべて整数の直角三
角形が
できます。3辺とも整数の三角形はピタゴラスの三角形といって、ピタゴラスの三角
形は上記で得られるもの以外はないんですよね。

あと
25^2-24^2=(25+24)（25-24)=49×１より　25^2=24^2+7^2となります。
ですから　61^2-60^2=（61+60）(61-60)=121から　61^2=60^2+11^2のようにできま
す。
つまり一辺が奇数のピタゴラス三角形は必ずできるんですね。
くわしい証明は省略します。
また、高校生でも　斜辺と他の一辺がわかってるときに、残りを出すのに
a^2-b^2=(a+b)(a-b)を
使えるものは少ないので、この計算をすると授業で感動してくれます。(^.^)