丂乽崱寧偺栤戣乿丂戞俁俉夞丂乮暯惉侾係擭侾侾寧乯
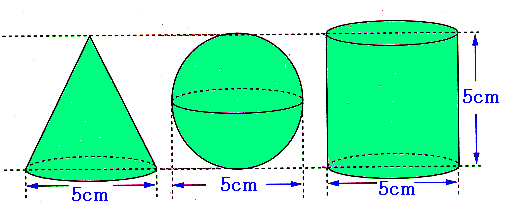
丂恾偺傛偆側乽墌偡偄乿丄乽媴乿丄乽墌拰乿偺宍傪偟偨愊傒栘偑偁傝傑偡丅
丂嵽幙乮枾搙乯偑摨偠偱偁傝丄戝偒側敔偺拞偵偙偺愊傒栘偑丄偄偔偮偐擖偭偰偄傑偡丅
丂慡懱偺愊傒栘偺廳偝偼丄墌偡偄侾屄偺廳偝偺偪傚偆偳侾侾侽屄暘偵側偭偨偲偄偆偙偲偱偡丅
偙偙偱栤戣偱偡丅
愊傒栘偺崌寁悢偑堦斣彮側偄応崌丄偦偺憤悢偼壗屄偵側傞偱偟傚偆偐丅
仸偨偩偟丄敔偺拞偵偼丄乽墌偡偄乿乽媴乿乽墌拰乿偺愊傒栘偼丄彮側偔偰傕侾屄偼娷傑傟偰偄傞偲偟傑偡丅 |
亙惓夝幰堦棗昞亜丂
丂丂丂丂丂丂丂丂丂丂丂
| 惓夝幰弴埵 |
丂丂丂丂値倎倣倕丂丂丂 |
丂丂儊乕儖摓拝擔帪丂丂 |
丂丂旛丂峫丂丂 |
| 丂侾 |
崅揷廋惉(廋摽妛堾)丂偝傫 | 2002/11/1丂0:03 | 暫屔導 |
| 丂俀 | Banyanyan丂偝傫 | 2002/11/1丂0:05 | 嫗搒晎丂 |
| 丂俁 | BEAN丂偝傫 | 2002/11/1丂0:06 | 丂 |
| 丂係 | Michael丂偝傫 | 2002/11/1丂0:11 | 丂 |
| 丂俆 |
BONZ丂偝傫 | 2002/11/1丂0:19 | Osaka/JAPAN |
| 丂俇 | N偺斶寑丂偝傫 | 2002/11/1丂0:35 | 暫屔導 |
| 丂俈 |
maruhagedon丂偝傫 | 2002/11/1丂2:28 | 丂 |
| 丂俉 | miya丂偝傫 | 2002/11/1丂5:38 | 丂 |
| 丂俋 | 怣嶰丂偝傫 | 2002/11/1丂8:14 | 僔儕僐儞僶儗乕偺廧恖丂 |
| 侾侽 | 宱桭夛偺恑嶌丂偝傫 | 2002/11/1丂10:42 | 嫗搒晎栘捗挰丂俇係嵨丂 |
| 侾侾 | teki丂偝傫 | 2002/11/1丂11:31 | 丂 |
| 侾俀 | 岼偺柌丂偝傫 | 2002/11/1丂18:59 | 媨忛導弌恎丂 |
| 侾俁 | 儌儖儌僢僩戝恇丂偝傫 | 2002/11/1丂19:30 | 儌儖儌僢僩墹崙丂 |
| 侾係 | Non丂偝傫 | 2002/11/1丂19:42 | 丂 |
| 侾俆 | ponta55555丂偝傫 | 2002/11/1丂23:19 | 丂 |
| 侾俇 | 榓媣 暯敧榊丂偝傫 | 2002/11/2丂0:34 | 暉壀嵼廧PG丂 |
| 侾俈 | ISAMU丂偝傫 | 2002/11/2丂8:57 | 嶰廳導丂 |
| 侾俉 | 側偵傢丂偝傫 | 2002/11/2丂9:54 | 惣媨巗丂 |
| 侾俋 | 僼傿儕僺儞偺戦丂偝傫 | 2002/11/2丂10:15 | 丂 |
| 俀侽 | 棟堦榊朧偪傖傫丂偝傫 | 2002/11/2丂16:46 | 嶳岥巗搾揷彫俇擭 |
| 俀侾 |
桳柍憡惗丂偝傫 | 2002/11/3丂17:40 | 恄撧愳導丄夛幮堳 |
| 俀俀 |
BossF丂偝傫 | 2002/11/3丂18:31 | 丂 |
| 俀俁 | 俵俙俼俷俼俬俶俤丂偝傫 | 2002/11/4丂13:28 | 暉壀導嵼廧丂朸恑妛弇島巘丂 |
| 俀係 | 傆偠偝偒偨偮傒丂偝傫 | 2002/11/4丂16:46 | 杒奀摴丂 |
| 俀俆 | 惔愳丂堢抝丂偝傫 | 2002/11/4丂23:22 | 峀搰巗丂 |
| 俀俇 | 僌儔儞僷丂偝傫 | 2002/11/4丂23:36 | 丂 |
| 俀俈 | 15KARATSOUL丂偝傫 | 2002/11/5丂15:21 | 暫屔導柉丂 |
| 俀俉 | 僗儌乕僋儅儞丂偝傫 | 2002/11/5丂22:52 | Jijy |
| 俀俋 |
僞儉儔側傫偱傕岺朳丂偝傫 | 2002/11/6丂21:46 | 丂 |
| 俁侽 | 兛攇丂偝傫 | 2002/11/8丂2:56 | 丂 |
| 俁侾 |
崅嫶丂摴峀丂偝傫 | 2002/11/8丂18:21 | 杒偺塀傟壠丂 |
| 俁俀 | 偁偁偁偁偁丂偝傫 | 2002/11/9丂11:47 | 丂 |
| 俁俁 | 埨妝崕壝丂偝傫 | 2002/11/12丂17:04 | 媨嶈導彫椦巗丂 |
| 俁係 | yuki丂偝傫 | 2002/11/14丂21:31 | 撧椙導丂 |
| 俁俆 | 僩僋僕丂偝傫 | 2002/11/29丂15:20 | 摽搰導丂壠掚嫵巘丂 |
| 俁俇 | N.Nishi丂丂偝傫 | 2002/11/30丂19:50 | 戝嶃晎丗拞妛嫵桜丂 |
摎偊偼俁俉屄偱偡丅崱夞傕僗儅乕僩側柾斖夝摎傪憲偭偰捀偒傑偟偨偺偱丄徯夘偝偣偰偄偨偩偒傑偡丅
亙倲倕倠倝丂偝傫傛傝亜
恾偺傛偆側墌悕丄媴丄墌拰偺懱愊偺斾偼丄侾丗俀丗俁偱偡偺偱丄
偙傟傪慻傒崌傢偣偰侾侾侽傪嶌傟偽偄偄栿偱偡丅
屄悢偑嵟彫偲側傞偺偼丄懱愊俁偺墌拰傪嵟傕懡偔巊偆応崌偱
偡偺偱丄侾侾侽亐俁亖俁俇梋傝俀傛傝丄墌拰偺屄悢偼俁俇屄埲撪
偱偡丅
彮側偔偲傕侾屄偼墌悕丄媴偑擖偭偰偄傞偺偱丄俁俇屄偺墌拰偑
擖偭偰偄傞応崌偼丄巆傝偺俀傪嶌傞偙偲偑偱偒傑偣傫丅
廬偭偰丄屄悢偑嵟彫偲側傞慻崌偣偼丄墌拰俁俆屄丄媴俀屄丄墌
悕侾屄偺崌寁俁俉屄偺応崌偲側傝傑偡丅
亙榓媣 暯敧榊丂偝傫亜
枾搙偑慡偰摍偟偄偺偱墌悕丄媴丄墌拰偺廳偝偺斾偼
5*(兾r^2)/3:4*(兾r^3)/3:5*兾r^2 (r=5/2)
佀1:2:3
偙偙偱墌悕丄媴丄墌拰偺屄悢傪偦傟偧傟兛,兝,兞偲偡傞偲
兛+2兝+3兞=110
乮兛,兝,兞偼帺慠悢乯丒丒丒嘆
兛+兝+兞偺嵟彫抣傪媮傔傞偺偱
嘆傪枮偨偡傛偆側兞偑庢傝摼傞嵟戝偺抣傪偲傟偽傛偄丅
兞=36偺偲偒
兛+2兝=2
偙傟偼嘆傪枮偨偝側偄偺偱揔偝側偄丅
兞=35偺偲偒
兛+2兝=5
偙傟傪枮偨偡(兛,兝)偺慻偱兛+兝偑嵟彫偵側傞慻傒崌傢偣偼
(兛,兝)=(1,2)
傛偭偰媮傔傞夝偼
兛+兝+兞=38(屄)
亙棟堦榊朧偪傖傫丂偝傫傛傝亜
墌悕乮C)丄媴乮S)丄墌拰乮P)偺懱愊偺斾偑丄杮栤偺応崌偵偼丄
侾丗俀丗俁偱偁傝丄偙傟偼廳偝偺斾偱傕偁傞丅埲壓C偺廳偝傪侾偲
偡傞丅
C,S,P偑偦傟偧傟倶丄倷丄倸屄偁傞偲偡傞偲丄
倶亄俀倷亄俁倸亖侾侾侽
屄悢傪側傞傋偔彮側偔偡傞偵偼丄倶傪側傞傋偔彮側偔丄倸傪側傞
傋偔懡偔偡傟偽傛偄丅
倶亖倷亖侾偱偼倸偑惍悢偱側偄偺偱丄倶亖侾丆倷亖俀傪峫偊傞丅
偙偺偲偒倸亖俁俆偱丄愊傒栘偺憤悢偼俁俉屄偵側傞丅埲壓倸傪侾
偯偮尭傜偟偰偄偔偲丄倶丄倷偑偦傟埲忋偵憹壛偡傞偙偲偑傢偐
傞丅
亙俵俙俼俷俼俬俶俤丂偝傫傛傝亜
夝愢丗墌悕偺懱愊乧兾亊5/2亊5/2亊5亊1/3亖125/12兾棫曽們倣
丂丂丂丂媴偺懱愊乧4/3亊兾亊5/2亊5/2亊5/2亖125/6兾棫曽們倣
丂丂丂墌拰偺懱愊乧兾亊5/2亊5/2亊5亖125/4兾棫曽們倣
丂丂丂偟偨偑偭偰丄懱愊斾墌悕丗媴丗墌拰亖1丗2丗3
丂丂丂偙偙偱丄懱愊偺崌寁偑墌悕侾侾侽屄暘偱偁傞偐傜丄
丂丂丂110亐3亖36屄乧2
丂丂丂偙偺偲偒丄媴傑偨偼墌悕偺偳偪傜偐偑侽屄偵側偭偰偟傑偆偺偱丄
丂丂丂墌拰偼35屄丄偦偆偡傞偲丄35亊3亖105丄110亅105亖5偲側傞偺丂
丂丂丂偱丄媴偼5亐2亖2屄乧1丄墌悕偼1屄偲側傞丅
丂丂丂傛偭偰丄崌寁屄悢偼35亄2亄1亖38屄丅
亙惔愳丂堢抝丂偝傫亜
丂懱愊斾丂侾丗俀丗俁
丂彮側偔偲傕偦傟偧傟侾屄偼偁傞丅丂俁屄丂巆傝丂侾侽係(屄暘)
丂倃丄倄丄倅丂旕晧惍悢
丂倃+俀*倄+俁*倅亖侾侽係
丂忦審偵傛傝丄
丂倃亖侽丄倄亖侾丄倅亖俁係
丂墌悕丂丂丂丂侾屄
丂媴丂丂丂丂丂俀屄
丂墌拰丂丂丂俁俆屄
丂嵟彫屄悢丂俁俉屄
亙僞儉儔側傫偱傕岺朳丂偝傫傛傝亜
嶰妏悕丄媴丄墌拰偺懱愊斾偼侾丗俀丗俁
乮墌悕偺懱愊傪侾偲偟偰峫偊傞丅乯
偟偨偑偭偰墌拰傪堦斣懡偔偲傞巇曽傪摎偊傟偽傛偄丅
俁俇屄偲傞偲墌悕侾侽俉屄暘偲側傝丄巆傝墌悕丄媴偺偳偪傜偐
堦庬椶偟偐偲傟側偄丅
偟偨偑偭偰丄墌拰偼俁俆屄偟偐偲傟側偄丅
懱愊偼丄俁俆亊俁亖侾侽俆偺墌悕暘
偺偙傝俆屄暘偺庢傝曽偼媴傪俀屄丄墌悕傪侾屄偲傞傛偆偵偡傟偽
嵟彫偺屄悢偲側傞丅
亙崅嫶丂摴峀丂偝傫丂傛傝亜
墌悕偺懱愊:(5/2)丱2兾亊5亊1/3=125兾/12
媴偺懱愊:4/3亊兾亊(5/2)丱3=125兾/6
墌拰偺懱愊:(5/2)丱2兾亊5=125兾/4
傛傝懱愊斾偼1:2:3
偙偺3偮傪慻傒崌傢偣偨傕偺偼桳柤側悢妛幰偺曟偵崗傑傟偰傞
偲偐暦偄偨偙偲偑偁傝傑偡丅(^丅^)
傛偭偰墌悕丄媴丄墌拰偺屄悢傪X,Y,Z偲偡傞偲x+2Y+3Z=110
Z偑嵟戝偵側傞偺偼丂110/3=36.66..偐傜
Z=36偱丂偙偺偲偒X+2Y=2丂Y=1丂X=0偑崌寁偑傕偭偲傕彮側偄丅
丂偟偐偟偙傟偼忦審偵崌偄傑偣傫丅偦偙偱
Z=35 偺偲偒丂X+2Y=5偱丂(X,Y)=(1,2)丂(3,1)
丂偙偺偆偪崌寁偑堦斣彮側偄偺偼丂(X,Y,Z)=(35,1,2)丂崌寁38屄
傑偨堦斒揑偵X+2Y+3Z=110偺偲偒丂
丂丂X+Y+Z
丂丂=X+Y+(110/3-1/3X-2/3Y)
丂丂=110/3+2/3X+1/3Y
丂丂>=110/3+2/3+1/3
丂丂=37.666偱偁傞偐傜丂X+Y+Z偺嵟彫偼38枹枮偵側傞偙偲偼側偄
丂埲忋偐傜崌寁38屄丂偲側傝傑偡丅
傑偨丂X+Y+Z=38傪枮偨偡傕偺偼丂X+2Y+3Z=110偐傜
2X+Y=4偲側傝丂(X,Y)=(1,2)傪摼傑偡偐傜丂(X,Y,Z)=(1,2,35)
偺傒偑夝偲側傞偙偲偑傢偐傝傑偡丅
亙yuki丂偝傫傛傝亜
墌悕傪倶屄丄媴傪倷屄丄墌拰傪倸屄偲偡傞偲丄
倶亄2y亄3z亖110
偙偙偱丄z偺嵟戝抣偼35偩偐傜丄z亖35
偙傟傪戙擖偟丄x亄2y亖5
偙偙偱丄y偺嵟戝抣偼2偩偐傜丄y亖2丄x亖1
傛偭偰憤榓偼x亄y亄z亖38屄
亙僩僋僕丂偝傫傛傝亜
壖掕丗枾搙亖侾
懱愊斾亖幙検斾丂丂墌悕丗媴丗墌拰亖侾丗俀丗俁
傛偭偰墌拰偺曄堟偼侾亝倶亝俁俇
偟偐偟丆奺愊傒栘偼嵟掅侾儢偢偮偼偄偭偰偄傞偺偩偐傜
墌拰俁俇屄傪揔墳偡傞偲俁亊俁俇亖侾侽俉偲側傝丆墌悕丆媴偺偄偢傟偐偑擖傜側偔側
傞丅
傛偭偰丆墌拰偺嵟戝抣傪俁俆偲偡傞偲俁亊俁俆亖侾侽俆偲側傝丆偺偙傝偼墌悕俆屄暘
偲側傞丅
媴偺悢傪俀儢偲偟偰傗傞偲俀亊俀亖係偱丆墌悕偼侾儢偲側傝丆
墌悕乮侾乯亄媴乮俀亊俀亖係乯亄墌拰乮俁亊俁俆亖侾侽俆乯亖墌悕侾侾侽屄暘
亪愊傒栘偺憤榓偼俁俉偑嵟彫偲側傞丅
