今月の問題」　第４1回　（平成１５年２月）

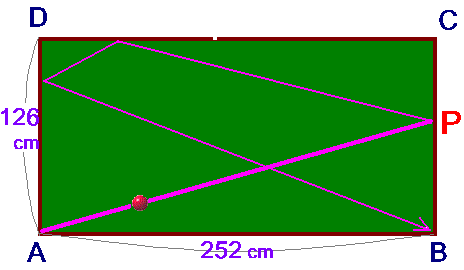
　上図のように、縦１２６cm、横２５２cmのビリヤード台があります。よしお君は、頂点Ａから打ち出した玉を、辺ＢＣ、ＤＣ、ＡＤではね返し、最後にＢの穴に入るように練習しています。

　ここで問題です。
　ＢＰの長さを何ｃｍにするとうまくいくでしょうか。

（※ただし、玉は辺以外では直進し、辺にあたると、あたった角度と等しい角度ではね返るものとします。）

＜正解者一覧表＞　 　　　　　　　　　　　
正解者順位 　　　　ｎａｍｅ　　　 　　メール到着日時　　 　　備　考　　
　１ 高田修成(修徳学院)　さん2003/2/1　0:03兵庫県
　２nobu　さん2003/2/1　0:04　
　３たかまつ　ろろ　さん2003/2/1　0:12神奈川県　
　４小金井のチンジャラ　さん2003/2/1　0:13東京都　
　５なにわ　さん2003/2/1　0:33西宮市　
　６信三　さん2003/2/1　1:42シリコンバレーの住人　
　７モルモット大臣　さん2003/2/1　7:17モルモット王国
　８N.Nishi　さん2003/2/1　8:45大阪府：中学教諭　
　９miya　さん2003/2/1　8:52熊本県　
１０BEAN　さん2003/2/1　10:40　
１１ISAMU　さん2003/2/1　14:23三重県
１２ 有無相生　さん2003/2/1　14:54神奈川県、会社員
１３経友会の進作　さん2003/2/1　15:01京都府木津町　６４歳　
１４teki　さん2003/2/1　16:41　
１５ミミズクはくず耳　さん2003/2/1　18:04横浜市　
１６巷の夢　さん2003/2/1　20:31宮城県出身　
１７yuki　さん2003/2/1　22:42奈良県　
１８asumi　さん2003/2/1　22:44　
１９清川　育男　さん2003/2/2　7:59広島市　
２０Michael　さん2003/2/2　9:59　
２１Banyanyan　さん2003/2/2　10:19　
２２浜田　明巳　さん2003/2/2　15:09　
２３ 呑　さん2003/2/2　18:04タダの酔っぱらい
２４かつひこ　さん2003/2/2　21:37　
２５MARORINE　さん2003/2/3　0:47　
２６理一郎坊ちゃん　さん2003/2/3　22:25山口市湯田小６年　
２７Nの悲劇　さん2003/2/4　0:02　
２８フィリピンの鷹　さん2003/2/4　11:56フィリピン在住
２９br8ker　さん2003/2/4　19:23東京都　受験生
３０うろつく者　さん2003/2/4　22:31中学生
３１安楽克嘉　さん2003/2/5　23:28　
３２ とんべい　さん2003/2/6　18:21大阪府
３３夢の旅人　さん2003/2/9　23:04　
３４kyoho　さん2003/2/10　9:25愛知県　大学生
３５勝浦捨てる造　さん2003/2/11　0:51河内の団塊おやじ　
３６スモークマン　さん2003/2/12　16:58放浪者　
３７TMOX　さん2003/2/12　21:46東京都
３８ 高橋　道広　さん2003/2/13　18:06北の隠れ家
３９モルモット増殖中　さん2003/2/16　23:43モルモット共和国　
４０ふじさきたつみ　さん2003/2/17　20:44北海道
４１幽玄太郎　さん2003/2/20　21:43　
４２バルバロッサ　さん2003/2/23　19:10神社
４３Hirobe　さん2003/2/24　15:293小、中教諭　
４４おーちゃん　さん2003/2/25　7:23群馬県　
４５ステップ　ばい　ステップ　さん　さん2003/2/28　21:26かけだし算数ファン
４６ mhayashi　さん2003/2/28　23:39大阪府

答えは、８４ｃｍでした。

以下のような考え方を送っていただきました。

＜mhayashi　さん＞
折り返してあるのを広げると答えが見える？【謎】

＜ステップ　ばい　ステップ　さん＞
長方形ＡＢＣＤを３つ横につなぎ、それを２段重ねにした
大長方形を使いました。反射角が等しいので、Ｂの穴に
入れるには「Ａから対角線の方向」に打ち出せばよいこと
が分かります。よって相似比から
ＢＰ＝（１２６×２）×１/３＝８４
となります。

＜おーちゃん　さん＞
 はねかえった辺で長方形を折り返す作業を繰り返し、AからBまで１直線
に進むようにする。
後は相似な三角形の辺の長さの比から
BP=126×2÷3=84cm

＜Hirobe　さん＞
 →３：↑１　であれば良いと思います。

＜高橋　道広　さん＞
BCを対称軸に長方形ABCDを対称移動すると玉はその対称移動した
長方形内を直進し、次にその対称移動した長方形をCDを対称軸と
して　対称移動し…と今まで図をかいていました。

しかし　このあいだ　次のような方法を発見しました。
あるいはみなさんご存知かも知れませんが　私は知らなかったの
でありました。
まあ　たいしたことではないけどね。(~_~;)

玉が上下方向に何回往復してるかと言うと、DCと１回あたって
るからADの２倍
左右方向に何回往復してるかというとAD,BCと２回あたってるから
ABの３倍となります。
これから　さきほどのようにぱたぱた長方形をひっくり返さなく
ても
玉の道筋はABの3倍を底辺　BCの3倍を高さとする直角三角形の
斜辺をたどることがわかるんです。
以上から　APはその大きな三角形の1/3の大きさで
BP=126×2÷3=84cmとなりました。

＜kyoho　さん＞
 縦方向に１２６＊２ｃｍ、横方向に２５２＊３ｃｍ進んだのと同じであ
る。（壁がなければその位置に到達するはず・・）。
このことより、はじめにぶつかった点Ｐの地点では、縦横ともに最終的
に進んだ距離の1/3だけ進んでいることになるため、ＢＰの長さは
126*2/3=８４ｃｍ。

＜MARORINE　さん＞
解説…球筋とＣＤとの交点をＱ、ＡＤとの交点をＲとすると、題意よ
り、△ＡＢＰ≡△ＢＡＲ、△ＱＣＰ≡△ＱＤＲ（いずれも１辺とその両
端の角がそれぞれ等しい）、また△ＡＢＰ（△ＢＡＲ）∽△ＱＣＰ（△
ＱＤＲ）（２組の角がそれぞれ等しい）となる。したがって、相似比Ａ
Ｂ：ＱＣ＝2：1より、ＢＰ：ＣＰ＝2：1であるから、ＢＰ＝126×2/3
＝84（ｃｍ）となる。

　

＜浜田　さん＞
ｖｉｓｕａｌ　basicのプログラムで玉の軌跡を解析していただきました。


 ＜ Banyanyan　さん＞
<図略>た.てと横の比は１：２
ＡＰ：ＰＢ＝２×３：１×２＝３：１
ＢＰ＝２５２÷３＝８４ｃｍ

＜yuki　さん＞
右、上、右の順に折り返すと、ボールの軌道は１直線となる
このときできる縦３２４、横７５６の三角形と三角形ＡＢＰは
相似だから、ＢＰ：２５２＝３２４：７５６
これを解き、ＢＰ＝８４cm

＜巷の夢　さん＞
対称を２回使い方程式を解きました。

＜ミミズクはくず耳　さん＞
 折り返した絵を描けば一目瞭然ですね。
126×2÷3 = 84

＜ｔｅｋｉさん＞
問題の長方形は縦と横の比が１：２ですので、ちょうど正方形を横に２つくっつけた形です。
問題の条件のように３クッションでポケットに入れるには、横２５２×３、縦１２６×２　だけ進める必要があります。
グラフ用紙に縦２個、横６個の正方形を描き、こうしてできる長方形の対角線を引くと、別添の図＜略＞のように、最初の長方形の縦２／３の点を通ることがわかります。
よって、求める長さは　１２６×２／３＝８４ｃｍ　です。

＜有無相生　さん＞
 長方形の縦の長さだけでできますね。
というか、図を正確に書くと、Pが、BCを2：1に内分する点であること
がわかります。＜N.Nishi　さんより＞
台を鏡のように何枚か並べて、直線を引きました。そして三角形の相似比で。