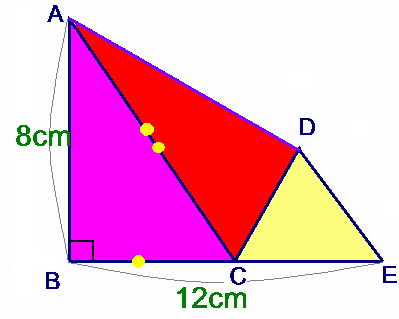
丂偙偺偲偒丄AB偲BE偺挿偝偑8cm偲12cm偵側傝傑偟偨丅
丂偙偙偱栤戣偱偡丅
丂仮ABC偲仮ACD偺柺愊偺榓偼壗們倣俀偵側傞偱偟傚偆偐丅

|
|
丂忋恾偺傛偆偵丄幬曈俙俠偲掙曈BC偺曈偺斾偑俀丗侾偺捈妏嶰妏宍ABC偲惓嶰妏宍CDE偑暲傫偱偄傑偡丅 丂偙偺偲偒丄AB偲BE偺挿偝偑8cm偲12cm偵側傝傑偟偨丅 丂偙偙偱栤戣偱偡丅 |
亙惓夝幰堦棗昞亜丂 丂丂丂丂丂丂丂丂丂丂丂
| 惓夝幰弴埵 | 丂丂丂丂値倎倣倕丂丂丂 | 丂丂儊乕儖摓拝擔帪丂丂 | 丂丂旛丂峫丂丂 |
| 丂侾 | 崅揷廋惉(廋摽妛堾)丂偝傫 | 2003/3/1丂0:05 | 暫屔導 |
| 丂俀 | 彫嬥堜偺僠儞僕儍儔丂偝傫 | 2003/3/1丂0:08 | 搶嫗搒丂 |
| 丂俁 | 偨偐傑偮丂傠傠丂偝傫 | 2003/3/1丂0:35 | 恄撧愳導丂 |
| 丂係 | 儌儖儌僢僩戝恇丂偝傫 | 2003/3/1丂3:10 | 儌儖儌僢僩墹崙丂 |
| 丂俆 | Banyanyan丂偝傫 | 2003/3/1丂3:16 | 嫗搒晎丂 |
| 丂俇 | 怣嶰丂偝傫 | 2003/3/1丂4:09 | 僔儕僐儞僶儗乕偺廧恖 |
| 丂俈 | teki丂偝傫 | 2003/3/1丂9:00 | |
| 丂俉 | 宱桭夛偺恑嶌丂偝傫 | 2003/3/1丂9:01 | 嫗搒晎栘捗挰丂俇係嵨 |
| 丂俋 | nobu丂偝傫 | 2003/3/1丂9:53 | 愇愳導 |
| 侾侽 | 埨妝崕壝丂偝傫 | 2003/3/1丂12:01 | 媨嶈導 |
| 侾侾 | 岼偺柌丂偝傫 | 2003/3/1丂12:08 | 媨忛導弌恎 |
| 侾俀 | ISAMU丂偝傫 | 2003/3/1丂13:16 | 嶰廳導 |
| 侾俁 | miya丂偝傫 | 2003/3/1丂14:33 | 孎杮導 |
| 侾係 | 偨偑偣傫丂偝傫 | 2003/3/1丂16:46 | 搶嫗搒 |
| 侾俆 | 桳柍憡惗丂偝傫 | 2003/3/1丂17:02 | 恄撧愳導丄夛幮堳 |
| 侾俇 | 傆偠偝偒偨偮傒丂偝傫 | 2003/3/1丂18:12 | 杒奀摴 |
| 侾俈 | 側偵傢丂偝傫 | 2003/3/1丂18:45 | 惣媨巗 |
| 侾俉 | 偐偮傂偙丂偝傫 | 2003/3/1丂22:58 | 暫屔敧幁 |
| 侾俋 | N.Nishi丂偝傫 | 2003/3/1丂23:28 | 戝嶃晎丗拞妛嫵桜 |
| 俀侽 | N偺斶寑丂偝傫 | 2003/3/2丂1:04 | 暫屔導 |
| 俀侾丂 | 愭惗偺嫵偊巕丂偝傫 | 2003/3/2丂13:07 | 暫屔抾栰 |
| 俀俀 | 惔愳丂堢抝丂偝傫 | 2003/3/2丂13:31 | 峀搰巗 |
| 俀俁 | Michael丂偝傫 | 2003/3/2丂16:01 | 丂 |
| 俀係 | br8ker丂偝傫 | 2003/3/3丂0:04 | 搶嫗庴尡惗巹戝崌奿 |
| 俀俆 | 崅栘懜枦丂偝傫 | 2003/3/3丂2:36 | 暉壀導嵼廧丄朸恑妛弇島巘 |
| 俀俇 | 僗儌乕僋儅儞丂偝傫 | 2003/3/4丂9:55 | 嶼悢岲偒俰倷 |
| 俀俈 | Non丂偝傫 | 2003/3/4丂10:04 | |
| 俀俉 | BONZ丂偝傫 | 2003/3/4丂17:02 | 夛幮仐惣媨 |
| 俀俋 | 僗僥僢僾丂偽偄丂僗僥僢僾丂偝傫 | 2003/3/4丂21:43 | 偐偗偩偟嶼悢僼傽儞 |
| 俁侽 | 儈儈僘僋偼偔偢帹丂偝傫 | 2003/3/5丂19:25 | 墶昹巗嵼廧 |
| 俁侾 | 棟堦榊朧偪傖傫丂偝傫 | 2003/3/5丂20:45 | 嶳岥巗搾揷彫俇擭 |
| 俁俀 | 撣丂偝傫 | 2003/3/6丂17:02 | 偄偮傕悓偭傁傜偄 |
| 俁俁 | 僼傿儕僺儞偺戦丂偝傫 | 2003/3/6丂15:49 | 僼傿儕僺儞嵼廧 |
| 俁係 | 崅嫶丂摴峀丂偝傫 | 2003/3/6丂16:31 | 杒偺塀傟壠 |
| 俁俆 | 偍乕偪傖傫丂偝傫 | 2003/3/7丂5:21 | 孮攏導 |
| 俁俇 | kyoho丂偝傫 | 2003/3/7丂15:38 | 垽抦導丂戝妛惗 |
| 俁俈 | 搚嫃丂愮庫丂偝傫 | 2003/3/8丂12:37 | 垽昋導丄傕偆偡偖僺僇僺僇偺拞妛惗丂 |
| 俁俉 | 屵擭偺偆傝傏偆丂偝傫 | 2003/3/8丂21:49 | 暉搰導丂 |
| 俁俋 | 昹揷丂柧枻丂偝傫 | 2003/3/10丂11:01 | 丂 |
| 係侽 | 乽晜楺偺娰乿娰挿丂偝傫 | 2003/3/13丂15:55 | 娾庤導 |
| 係侾 | miyuki丂偝傫 | 2003/3/13丂19:45 | 怴妰導丂嫵堳丂彈丂 |
| 係俀 | 儐僂僇儕丂偝傫 | 2003/3/14丂0:08 | 暉堜導撝夑巗丂壣側庡晈 |
| 係俁 | yuki丂偝傫 | 2003/3/14丂13:59 | 撧椙導丂 |
| 係係 | LIA丂偝傫 | 2003/3/17丂22:09 | 戝嶃恖乮丱丱乯丂 |
| 係俆 | 垻媣崻丂偝傫 | 2003/3/18丂22:08 | 柤悾巗 |
| 係俇 | 柤慜側偟丂偝傫 | 2003/3/21丂0:01 | 楢棈壓偝偄丂 |
| 係俈 | 彑塝幪偰傞憿丂偝傫 | 2003/3/21丂21:51 | 崱栭偼悓偭暐偄 |
| 係俉 | 側偐丂偝傫 | 2003/3/25丂23:24 | 杒奀摴 |
| 係俋 | isami丂偝傫 | 2003/3/26丂0:14 | 崅抦導 |
| 俆侽 | kasama丂偝傫 | 2003/3/26丂22:48 | 丂 |
摎偊偼係俉們倣俀偱偟偨丅
師偺傛偆側慺揋側夞摎傪捀偒傑偟偨丅
亙Banyanyan丂偝傫亜
俙俠丗俠俛亖俀丗侾傛傝丄佢俙俠俛亖俇侽亱
傛偭偰丄俙俠//俢俤偩偐傜丄
仮俙俠俢亖仮俙俠俤
仮俙俛俠亄仮俙俠俢亖仮俙俛俠亄仮俙俠俤
亖仮俙俛俤
亖侾俀亊俉亐俀
亖係俉們倣俀
亙teki丂偝傫亜
嶰妏宍ABC偼丄惓嶰妏宍偺敿暘偺嶰妏宍偱偡偺偱妏ACB偼俇侽搙偱偡丅
廬偭偰妏ACD傕俇侽搙乮侾俉侽-俇侽-俇侽乯偲側傝丄AC傪愜傝栚偲偟偰愜傝曉偣偽丄揰D偼BC忋偵偔傞偙偲偑傢偐傝傑偡丅
廬偭偰丄俀偮偺嶰妏宍偺崅偝偼摍偟偔丄俉們倣偲側傝傑偡丅
掙曈偺崌寁偑侾俀們倣偱偡偺偱丄柺愊偺崌寁偼丄
侾俀亊俉亐俀亖係俉們倣2丂偱偡丅
亙傆偠偝偒偨偮傒丂偝傫亜 俙俠丗俛俠亖俀丗侾偐傜佢俙俠俛亖俇侽搙丄佢俙俤俠亖俇侽偩偐傜 俙俠暯峴俢俤側偺偱丄仮俙俠俢亖仮俙俠俤丂丂偩偐傜丄媮傔傞柺愊偺榓 偼丄仮俙俛俤亖係俉
亙傆偠偐傢丂偝傫亜 俛俠丗俙俠亖侾丗俀傛傝佢俙俛俠亖俇侽亱 傑偨仮俠俢俤偼惓嶰妏宍側偺偱佢俠俢俤亖俇侽亱 傛偭偰佢俙俠俢亖俇侽亱偵側傞丅 傑偨俙俠偼嫟捠偺偨傔曈俠俢傪掙曈偲偟偨偲偒仮俙俠俢偺崅偝偼俉cm偵側傞丅 傛偭偰仮俙俛俠亄仮俙俠俢亖俉亊侾俀亐俀亖係俉
亙崅栘懜枦丂偝傫亜 仮俙俛俠偼1丗2丗儖乕僩3偺捈妏嶰妏宍偱偁傞偐傜丄 佢俙俠俛亖60亱丅傑偨丄仮俠俢俤偼惓嶰妏宍偱偁傞偐傜丄 佢俢俤俠亖60亱丅傛偭偰丄佢俙俠俛亖佢俢俤俠偲側傝丄摨埵妏偑 摍偟偄偐傜丄俙俠//俢俤丅偙偙偱丄2揰俙丆俤傪寢傃丄曈俠俢偲 偺岎揰傪俥偲偡傞偲丄摍愊曄宍偵傛傝丄仮俙俥俢亖仮俠俥俤丅丂 傛偭偰丄仮俙俛俠亄仮俙俠俢亖仮俙俛俠亄仮俙俥俠亄仮俙俥俢丂 丂丂丂丂亖仮俙俛俠亄仮俙俥俠亄仮俠俥俤亖仮俙俛俤偲側傞丅丂丂丂丂丂 丂丂丂偟偨偑偭偰丄媮傔傞柺愊偼丄俛俤亊俛俙亐2亖12亊8亐2亖48們倣2
亙惔愳丂堢抝丂偝傫亜 挿曽宍ABEF傪峫偊傞丅ED偺墑挿慄偲AF偲偺岎揰傪G偲偡傞丅 俁妏宍ABC==俁妏宍EFG 巐妏宍ACEG偼暯峴巐曈宍丅 俁妏宍DAC偼暯峴巐曈宍ACEG偺敿暘丅 偟偨偑偭偰丄媮傔傞恾宍偺柺愊偼挿曽宍ABEF偺敿暘丅 俉亊侾俀亐俀亖係俉
亙僗僥僢僾丂偽偄丂僗僥僢僾丂偝傫亜
俙俠丗俛俠亖俀丗侾傛傝
捈妏嶰妏宍俙俛俠偼俙俠傪侾曈偲偡傞惓嶰妏宍偺敿暘偵側傞丅傛偭偰
佢俙俠俛亖俇侽亱
佢俢俤俠=俇侽亱側偺偱
俙俠//俢俤
暯峴慄偵傛傞摍愊堏摦偵傛傝
仮俙俠俢亖仮俙俠俤
偟偨偑偭偰
仮俙俛俠亄仮俙俠俢亖仮俙俛俠亄仮俙俠俤
丂丂丂丂丂丂丂丂丂丂丂亖仮俙俛俤
丂丂丂丂丂丂丂丂丂丂丂亖侾俀亊俉亐俀
丂丂丂丂丂丂丂丂丂丂丂亖係俉(cm丱2)
(摎偊乯丂係俉們倣丱2
丂
亙儈儈僘僋偼偔偢帹丂偝傫亜 仮ABC偼惓嶰妏宍偺敿暘偺嶰妏掕婯宆側偺偱丄佢ACB偼60搙丅 佢DCE傕60搙側偺偱丄佢ACD傕60搙丅偟偨偑偭偰丄 仮ACD傪C傪拞怱偵塃偵60搙夞揮偝偣偨仮A'CD'偼仮A'CE偲廳側傞丅 仮ACA'偑惓嶰妏宍偵側傞偺偱丄仮A'CE偺CE傪掙曈偲偟偨崅偝 乮A'偐傜CE偵崀傠偟偨悅慄偺挿偝乯偼AB偲摨偠8cm丅 偟偨偑偭偰丄仮ABC+仮ACD = 仮ABC亄仮A'CE 偼 AE傪懳妏慄偲偡傞挿曽宍ABEF偺敿暘 = 8亊12亐2 = 48
亙棟堦榊朧偪傖傫丂偝傫亜 妏俙俠俛亖俇侽搙丅俠俢偺墑挿忋偵俥傪偲傝丄嶰妏宍俙俠俥傪 惓嶰妏宍偵側傞傛偆偵偡傞偲丄俙俥偲俛俠偼暯峴丅 俛俠亖倶偲偡傞偲丄俉丱俀亄倶丱俀亖乮俀倶乯丱俀偩偐傜丄 倶偼嬶懱揑悢抣乮倶亖俉乛俽倯倰倲俁乯丅傛偭偰丄嶰妏宍俙俠俥 傕媮傑傞丅 嶰妏宍俙俠俢丗嶰妏宍俙俢俥亖俙俢丗俢俥 丂丂丂丂丂丂丂丂丂丂丂丂丂亖侾俀亅倶丗俁倶亅侾俀
亙僼傿儕僺儞偺戦丂偝傫亜 曈BC偺挿偝傪倎偲偡傞偲 仮ABC傪AC偵偦偭偰愜傝曉偟偰偱偒傞巐妏宍ABCB'偺柺愊偼 係倎倶俀 仮ADB'偺柺愊偼仮ABCx(DB'/CB') 係倎倶乮俀倎亅侾俀乯乛倎 巐妏宍ABCD偺柺愊偼丂巐妏宍ABCB' 亅丂仮ADB' 係倎倶俀亅係倎倶乮俀倎亅侾俀乯乛倎 亖係俉
亙kyoho丂偝傫亜 嚈ABC偺娭學傛傝丄BC=俉/併俁丄佢ACB=俇侽亱丅偙傟傛傝丄佢ACB=佢 DEC側偺偱丄AC//DE丅 埲忋傛傝丄嚈ACE偺柺愊偲嚈ACD偺柺愊偼摍偟偄丅傛偭偰丄媮傔傞柺愊偼 嚈ABE偺柺愊偵摍偟偄偐傜丄俉亊侾俀亐俀亖係俉cm^2
亙搚嫃丂愮庫丂偝傫亜 佢ACB=佢DEC=60搙丄傛偭偰AC偲DE偼暯峴丅廬偭偰仮ADC偲仮AEC偼 掙曈AC偑嫟捠偱崅偝偺摍偟偄嶰妏宍偱偁傞偐傜偦偺柺愊偼摍偟 偄丅傛偭偰仮ABC+仮ACD=仮ABC+仮AEC=仮ABE=8亊12亐2亖48
亙屵擭偺偆傝傏偆丂偝傫亜 仮俙俛俠亖俁俀併俁乛俁乮們倣丱俀乯丄 仮俙俠俢亖丂侾乛俀丂亊丂乮侾俀亅俉併俁乛俁乯丂亊丂侾俇併俁乛俁 丂丂丂丂亊丂倱倝値俇侽亱 丂丂丂丂亖係乮侾俀亅俉併俁乛俁乯乮們倣丱俀乯 亪丂仮俙俛俠亄仮俙俠俢亖係俉乮們倣丱俀乯丂乧乮摎乯丂
亙昹揷柧枻丂偝傫亜 VBscript偱嶌傝傑偟偨丏摎偼48cm2偱偡丏 丂壗偺岺晇傕側偄偮傑傜側偄僗僋儕僾僩偱偡丏 '0303.vbs AB=8 BE=12 'sqr(3)*BC=AB BC=AB/sqr(3) CE=BE-BC 'H:CE偺拞揰 DH=sqr(3)*.5*CE CH=CE*.5 BH=BC+CH '榓=仮ABC+仮ACD=戜宍ABHD-仮DCH wa=.5*(AB+DH)*BH-.5*CH*DH msgbox "榓="&wa&"cm2", vbinformation, "崱寧偺栤戣丂戞係俀夞乮暯惉侾俆擭俁寧乯"
亙LIA丂偝傫亜 偙偺慜偺丄恾傪尒偰娫堘偊偰偄傞偙偲婥偯偒傑偟偨乮丱丱丟乯 庢傝姼偊偢丄 俠俤偵岦偐偭偰捀揰俢偐傜悅慄傪堷偄偰岎揰傪俹偲偟偰丄 仮俙俛俠亄仮俙俠俢亖仩俙俛俹俢亅仮俠俢俤/俀 仩俙俛俹俢佮俆俋.俉們倣2 仮俠俢俤佮俀俁.俇們倣2 戙擖乣 仩俙俛俹俢亅仮俠俢俤/俀亖俆俋.俉亅俀俁.俇/俀 丂丂丂丂丂丂丂丂丂丂丂 亖係俉.侽 傛偭偰丄丂仮俙俛俠亄仮俙俠俢亖係俉.侽們倣2
亙kasama丂偝傫亜 - 2003/03/26 23:10 - 揰D偐傜曈CD偵悅捈偵壓傠偟偨揰傪D'偲偟偰丄戜宍ABD'D偺柺愊偐傜惓嶰妏宍CDE偺柺愊偺敿暘傪堷偄偰媮傔傑偟偨丅 戜宍ABD'D偺柺愊=2(31併3+36)/3 嶰妏宍CDE偺柺愊=(124併3-144)/3 媮傔傞柺愊=2(31併3+36)/3 - (124併3-144)/3亊1/2=48
丂
丂
亙側偐丂偝傫亜
師偺傛偆側偄恾偱帵偟偰偄偨偩偒傑偟偨丅

