傑偨懳妏慄俙俠偲俛俤偲偺岎揰偑揰俥偱偡丅丂傑偨丄慄暘俙俤偲慄暘俢俥偺岎揰傪俧偲偟傑偡丅
丂偙偙偱栤戣偱偡丅
丂慄暘FG偲慄暘俢俧丂偺斾偼偄偔傜偵側傞偱偟傚偆偐丅丂俥俧丗DG丂偱摎偊偰偔偩偝偄丅
乽

|
|
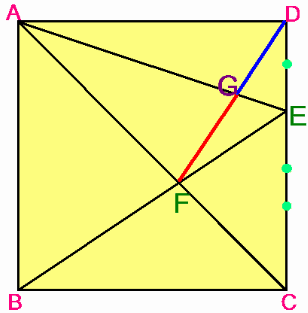
丂忋恾偺傛偆偵丄惓曽宍ABCD偑偁傝傑偡丅曈俠俢忋偵俀丗侾偵暘偗傞揰俤偑偁傝傑偡丅 傑偨懳妏慄俙俠偲俛俤偲偺岎揰偑揰俥偱偡丅丂傑偨丄慄暘俙俤偲慄暘俢俥偺岎揰傪俧偲偟傑偡丅 丂偙偙偱栤戣偱偡丅 |
亙惓夝幰堦棗昞亜丂 丂丂丂丂丂丂丂丂丂丂丂
| 惓夝幰弴埵 | 丂丂丂丂値倎倣倕丂丂丂 | 丂丂儊乕儖摓拝擔帪丂丂 | 丂丂旛丂峫丂丂 |
| 丂侾 | 崅揷廋惉(廋摽妛堾)丂偝傫 | 2003/4/1丂0:02 | 暫屔導 |
| 丂俀 | 彫嬥堜偺僠儞僕儍儔丂偝傫 | 2003/4/1丂0:05 | 搶嫗搒丂 |
| 丂俁 | 偨偐傑偮丂傠傠丂偝傫 | 2003/4/1丂0:16 | 恄撧愳導丂 |
| 丂係 | 搚嫃 愮庫丂偝傫 | 2003/4/1丂0:26 | 垽昋導丂拞堦丂 |
| 丂俆 | Michael丂偝傫 | 2003/4/1丂0:37 | 丂 |
| 丂俇 | 徝撿懢榊丂偝傫 | 2003/4/1丂0:46 | 弶嶲壛丂 |
| 丂俈 | 怣嶰丂偝傫 | 2003/4/1丂0:54 | 僔儕僐儞僶儗乕偺廧恖丂 |
| 丂俉 | Banyanyan丂偝傫 | 2003/4/1丂1:27 | 嫗搒晎丂 |
| 丂俋 | MARORINE丂偝傫 | 2003/4/1丂2:18 | 暉壀導嵼廧丄朸恑妛弇島巘丂 |
| 侾侽 | 屵擭偺偆傝傏偆丂偝傫 | 2003/4/1丂2:20 | 丂 |
| 侾侾 | 撣丂偝傫 | 2003/4/1丂5:36 | 丂 |
| 侾俀 | miya丂偝傫 | 2003/4/1丂6:13 | 丂 |
| 侾俁 | 側偐丂偝傫 | 2003/4/1丂10:56 | 杒奀摴丂 |
| 侾係 | 彑塝幪偰傞憿丂偝傫 | 2003/4/1丂12:12 | 戝嶃拞壨撪孲丂 |
| 侾俆 | BEAN丂偝傫 | 2003/4/1丂15:33 | 丂 |
| 侾俇 | teki丂偝傫 | 2003/4/1丂17:53 | 丂 |
| 侾俈 | 僗儌乕僋儅儞丂偝傫 | 2003/4/2丂20:09 | 丂 |
| 侾俉 | kasama丂偝傫 | 2003/4/1丂21:07 | 榓壧嶳丂 |
| 侾俋 | ISAMU丂偝傫 | 2003/4/1丂23:10 | 嶰廳導丂 |
| 俀侽 | 惔愳丂堢抝丂偝傫 | 2003/4/1丂23:12 | 峀搰巗丂 |
| 俀侾 | 桳柍憡惗丂偝傫 | 2003/4/1丂23:12 | 恄撧愳導丄夛幮堳丂 |
| 俀俀 | 側偵傢丂偝傫 | 2003/4/1丂23:59 | 惣媨巗丂 |
| 俀俁 | 宱桭夛偺恑嶌丂偝傫 | 2003/4/2丂5:26 | 嫗搒晎栘捗挰丂俇係嵨丂 |
| 俀係 | 岼偺柌丂偝傫 | 2003/4/2丂7:46 | 媨忛導弌恎丂 |
| 俀俆 | 儌儖儌僢僩戝恇丂偝傫 | 2003/4/2丂8:29 | 儌儖儌僢僩墹崙丂 |
| 俀俇 | nobu丂偝傫 | 2003/4/2丂14:5 | 愇愳導丂 |
| 俀俈 | 倝倱倎倣倝丂偝傫 | 2003/4/5丂22:31 | 崅抦導丄夛幮堳丂 |
| 俀俉 | 傎偘丂偝傫 | 2003/4/9丂13:03 | 杒偺塀傟壠丂 |
| 俀俋 | N偺斶寑丂偝傫 | 2003/4/9丂22:17 | 暫屔導丂 |
| 俁侽 | TOMOAKI丂偝傫 | 2003/4/11丂13:22 | 戝暘導丂 |
| 俁侾 | 僥儌丂偝傫 | 2003/4/12丂12:33 | 峀搰巗偺旤楅偑媢 |
| 俁俀 | 僂儖僩儔儅儞丂偝傫 | 2003/4/12丂侾9:03 | 丂 |
| 俁俁 | 昹揷柧枻丂偝傫 | 2003/4/14丂12:59 | 丂 |
| 俁係 | 儈儈僘僋偼偔偢帹丂偝傫 | 2003/4/14丂19:23 | 墶昹巗嵼廧丂 |
| 俁俆 | 僗僥僢僾丂偽偄丂僗僥僢僾丂偝傫 | 2003/4/15丂21:44 | 嬱偗弌偟嶼悢僼傽儞丂 |
| 俁俇 | 塱峅 悽擵夘丂偝傫 | 2003/4/18丂15:32 | 搶嫗搒丂 |
| 俁俈 | 2寧2擔丂偝傫 | 2003/4/20丂20:32 | 愒曚孲 |
| 俁俉 | 埨妝丂偝傫 | 2003/4/21丂22:35 | 媨嶈導丂 |
| 俁俋 | yuki丂偝傫 | 2003/4/25丂20:07 | 撧椙導 |
| 係侽 | 傆偠偝偒偨偮傒丂偝傫 | 2003/4/29丂19:50 | 杒奀摴丂 |
摎偊偼俇丗俆偱偟偨丅
丂
宖帵斅偵夝朄傪婰擖偟偰偄偨偩偒傑偟偨丅
儈儈僘僋偼偔偢帹偝傫 - 2003/04/14 19:23 -
DF偺墑挿偲AB偺墑挿偺岎揰傪H偲偡傞偲丄
EC:AB = 2:3 偐傜 EF:BF = DF:FH = DE:BH = 2:3
偟偨偑偭偰丄DE:AH = (1/3):{1+(1/3)*3/2} = 2:9
偟偨偑偭偰丄DF:FH = 2:9
傑偨丄DF:FH = 2:3 偩偐傜丄
FG:GD = (GH-FG):GD = {(9/11)-(3/5)}:(2/11) = 6:5
偲弌偟傑偟偨丅
崅嫶丂摴峀偝傫 - 2003/04/09 13:01 -
曗彆慄傪棙梡偟傑偟偨丅
偨偐傑偮丂傠傠丂偝傫偲偪傚偭偲堘偆偺偱彂偒傑偡丅
F傪偲偍傝AB偵暯峴側捈慄偲AE偺岎揰傪P偲偟傑偡丅
嶰妏宍ABF偲嶰妏宍CEF偼憡帡偱偡偐傜丂AF:FC=AB:CE=3:2
嶰妏宍AFP偲嶰妏宍ACE偼憡帡偱偡偐傜丂FP:CE=AF:AC=3:5
嶰妏宍PFG偲嶰妏宍EDG偼憡帡偱偡偐傜丂
FG:DG=PF:ED=3/5CE:1/2CE=6:5
丂偲偟傑偟偨丅
桳柍憡惗偝傫 - 2003/04/01 23:10 -
夝愅揑偵夝偒傑偟偨丅
丂
Banyanyan偝傫 - 2003/04/01 21:54 -
儊僱儔僂僗偼儅僀僫乕側傫偱偡偐偹丅
偩偲偟偨傜丄僠僃僶偺掕棟偺曽偑儊僕儍乕側傫偱偟傚偆偐丅
仮俙俧俢丗仮俙俧俠亖俢俤丗俤俠亖侾丗俀
仮俙俧俢丗仮俠俢俧亖俙俥丗俥俠亖俙俛丗俠俤亖俁丗俀
傛偭偰丄
仮俙俧俢丗仮俙俧俠丗仮俠俢俧亖俁丗俇丗俀
俥俧丗俧俢亖仮俙俧俠丗乮仮俙俧俢亄仮俠俢俧乯亖俇丗乮俁亄俀乯亖俇丗俆
kasama偝傫 - 2003/04/01 21:04 -
巹傕儊僱儔僂僗傪傛偔抦傜側偄偺偱丄嵗昗偱夝偒傑偟偨丅
丂
偨偐傑偮丂傠傠偝傫 - 2003/04/01 14:41 -
妎偊偨偰偺儊僱儔僂僗偱夝偒傑偟偨偑
暿夝偲偟偰
俥傪捠傝俙俤偵暯峴側慄偲俢俠偲偺岎揰傪俫偲偡傞偲
俠俤丗俙俛亖俠俥丗俙俥亖俠俫丗俫俤亖俀丗俁
俠俤丗俤俢亖俀丗侾傛傝
俠俫丗俫俤丗俤俢亖係丗俇丗俆
傛偭偰
俫俤丗俤俢亖俥俧丗俧俢亖俇丗俆
teki偝傫 - 2003/04/01 13:15 -
偼傗偭偰傑偡偹丅
愭廡偺偳偙偐偺栤戣偱傕偁傝傑偟偨偹丅
幚偼丄巹偼儊僱儔僂僗傪傛偔抦傜側偄傕傫偱丄嵗昗偱夝偒傑偟偨丅
丂
miya偝傫 - 2003/04/01 06:09 -
儊僱儔僂僗偺掕棟偱夝偒傑偟偨丅
丂
Banyanyan偝傫 - 2003/04/01 01:36 -
儃僋偼杮摉偼偙偪傜偱夝偒傑偟偨丅
俥俧丗俧俢
亖仮俙俥俤丗仮俙俤俢
亖仮俙俠俤亊俁乛俆丗仮俙俤俢
亖仮俙俤俢亊俀亊俁乛俆丗仮俙俤俢
亖俇丗俆
愭偺18傕偙偪傜傕丄仮俙俛俥佷仮俠俤俥傪巊偭偰偄傑偡偑丅
丂
儊僱儔僂僗偺掕棟 Banyanyan偝傫 - 2003/04/01 01:31 -
俧俢乛俥俧亊俤俠乛俢俤亊俙俥乛俠俙亖侾
俧俢乛俥俧亊丂俀乛丂侾亊丂俁乛丂俆亖侾
俧俢乛俥俧亖俆乛俇
仸倷倳倠倝偝傫傕摨偠夝朄偱儊乕儖傪偄偨偩偒傑偟偨丅
丂
亙僗僥僢僾丂偽偄丂僗僥僢僾丂偝傫亜
摎偊丂俥俧丗俢俧亖俇丗俆
仮俙俢俤丗仮俛俠俤亖侾丗俀
丂丂丂丂丂丂丂丂丂亖俆丗侾侽丒丒丒丒丒嘆
俥俧丗俢俧亖仮俙俤俥丗仮俙俤俢
丂丂丂丂丂亖仮俛俠俥丗仮俙俢俤丒丒丒丒丒嘇
仮俛俠俥丗仮俠俤俥亖俛俥丗俤俥
丂丂丂丂丂丂丂丂丂亖俙俛丗俠俤丂乮仮俙俛俥佷仮俠俤俥傛傝乯
丂丂丂丂丂丂丂丂丂亖俁丗俀
傛傝
俛俥丗俤俥亖俁丗俀
俛俥丗俛俤亖俁丗俆
傛偭偰
仮俛俠俤丗仮俛俠俥亖俛俤丗俛俥
丂丂丂丂丂丂丂丂丂亖丂俆丗丂俁
丂丂丂丂丂丂丂丂丂亖侾侽丗丂俇丒丒丒丒丒嘊
嘆偲嘊傛傝
仮俛俠俥丗仮俙俢俤亖俇丗俆丒丒丒丒丒嘋
嘇偲嘋傛傝
俥俧丗俢俧亖俇丗俆丒丒丒丒丒摎偊
偦偺懠
亙埨妝偝傫亜
揰G偲揰F偐傜曈AD傊悅慄傪
偍傠偡峫偊曽偱
捈妏嶰妏宍ADE偲俁丗侾偺憡帡側
捈妏嶰妏宍傪峫偊傞偲
偙偨偊偼
俇丗俆偱偡丅
亙昹揷柧枻偝傫亜
僾儘僌儔儉揑偵夝愅偟偰偄偨偩偒傑偟偨丅
丂
丂