丂傑偨丄壓掙BC偵暯峴慄倣値傪傂偔偲丄戜宍俙倣値俢偲戜宍値俛C値偺柺愊偑摍偟偔側傝傑偟偨丅
丂偙偙偱栤戣偱偡丅
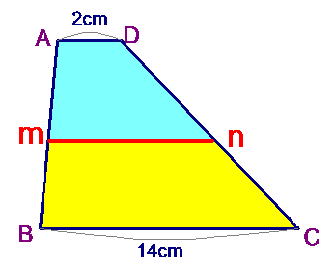
丂慄暘倣値丂偺挿偝偼壗們倣偵側傞偱偟傚偆偐丅丂
丂
乽

|
|
丂忋恾偺傛偆側丄戜宍ABCD偑偁傝傑偡丅忋掙AD偺挿偝偲壓掙B俠偺挿偝傪應傞偲俀們倣偲侾係們倣偵側傝傑偟偨丅 丂傑偨丄壓掙BC偵暯峴慄倣値傪傂偔偲丄戜宍俙倣値俢偲戜宍値俛C値偺柺愊偑摍偟偔側傝傑偟偨丅 丂偙偙偱栤戣偱偡丅 |
亙惓夝幰堦棗昞亜丂 丂丂丂丂丂丂丂丂丂丂丂
| 惓夝幰弴埵 | 丂丂丂丂値倎倣倕丂丂丂 | 丂丂儊乕儖摓拝擔帪丂丂 | 丂丂旛丂峫丂丂 |
| 丂侾 | 嵅摗 峀愰丂偝傫 | 2003/5/1丂0:00 | 搶嫗搒丂 |
| 丂俀 | 偨偐傑偮丂傠傠丂偝傫 | 2003/5/1丂0:08 | 恄撧愳導丂 |
| 丂俁 | 撣丂偝傫 | 2003/5/1丂0:09 | 偨偩丂 |
| 丂係 | 崅揷廋惉(廋摽妛堾)丂偝傫 | 2003/5/1丂0:14 | 暫屔導 |
| 丂俆 | nobu丂偝傫 | 2003/5/1丂0:26 | 愇愳導丂 |
| 丂俇 | Michael丂偝傫 | 2003/5/1丂0:32 | 丂 |
| 丂俈 | 搚嫃 愮庫丂偝傫 | 2003/5/1丂0:41 | 垽昋導丂拞堦丂 |
| 丂俉 | 儌儖儌僢僩戝恇丂偝傫 | 2003/5/1丂0:43 | 儌儖儌僢僩墹崙丂 |
| 丂俋 | 彑塝幪偰傞憿丂偝傫 | 2003/5/1丂0:51 | 戝嶃晎拞壨撪孲丟揷幧幰丂 |
| 侾侾 | makisen丂偝傫 | 2003/5/1丂1:40 | 垽抦導丂戝妛惗丂棨忋晹強懏 |
| 侾侾 | 怣嶰丂偝傫 | 2003/5/1丂2:53 | 僔儕僐儞僶儗乕偺廧恖丂 |
| 侾俀 | miya丂偝傫 | 2003/5/1丂5:52 | 丂 |
| 侾俁 | 岼偺柌丂偝傫 | 2003/5/1丂11:45 | 媨忛導弌恎丂 |
| 侾係 | 宱桭夛偺恑嶌丂偝傫 | 2003/5/1丂12:02 | 嫗搒晎栘捗挰丂俇係嵨丂 |
| 侾俆 | TOMOAKI丂偝傫 | 2003/5/1丂12:05 | 戝暘導丂 |
| 侾俇 | Banyanyan丂偝傫 | 2003/5/1丂14:31 | 嫗搒晎丂 |
| 侾俈 | 昹揷丂柧枻丂偝傫 | 2003/5/1丂16:51 | 丂 |
| 侾俉 | kasama丂偝傫 | 2003/5/1丂20:15 | 榓壧嶳導僾儘僌儔儅丂 |
| 侾俋 | 側偵傢丂偝傫 | 2003/5/1丂20:28 | 惣媨巗丂 |
| 俀侽 | ISAMU丂偝傫 | 2003/5/1丂21:27 | 嶰廳導丂 |
| 俀侾 | 僼傿儕僺儞偺戦丂偝傫 | 2003/5/1丂22:19 | 丂 |
| 俀俀 | 桳柍憡惗丂偝傫 | 2003/5/1丂22:21 | 恄撧愳導丄夛幮堳 |
| 俀俁 | 側偐丂偝傫 | 2003/5/1丂22:55 | 杒奀摴 |
| 俀係 | 倲倕倠倝丂偝傫 | 2003/5/1丂23:05 | 丂 |
| 俀俆 | MARORINE丂偝傫 | 2003/5/2丂0:05 | 暉壀導嵼廧丄朸恑妛弇島巘丂 |
| 俀俇 | 屵擭偺偆傝傏偆丂偝傫 | 2003/5/2丂7:14 | 暉搰導 |
| 俀俈 | 僥儌丂偝傫 | 2003/5/2丂19:55 | 峀搰巗偺旤楅偑媢丂 |
| 俀俉 | 垻媣崻岶媂丂偝傫 | 2003/5/2丂22:16 | 墏旤偵廧傫偱傑偡 |
| 俀俋 | 埨妝丂偝傫 | 2003/5/3丂0:07 | 丂 |
| 俁侽 | 僗僥僢僾丂偽偄丂僗僥僢僾丂偝傫 | 2003/5/3丂11:56 | 搶嫗搒 |
| 俁侾 | N偺斶寑丂偝傫 | 2003/5/3丂17:30 | 暫屔導丄朸弇島巘丂 |
| 俁俀 | 傆偠偝偒偨偮傒丂偝傫 | 2003/5/4丂9:33 | 杒奀摴丂 |
| 俁俁 | 偝偝丂偝傫 | 2003/5/5丂10:14 | 係侾嵨丂 |
| 俁係 | expo丂偝傫 | 2003/5/6丂22:14 | 杒奀摴丂 |
| 俁俆 | isami丂偝傫 | 2003/5/10丂17:44 | 崅抦導丂 |
| 俁俇 | 偁偛傜丂傒偺傞丂偝傫 | 2003/5/12丂12:12 | 暉壀導暉壀巗丂 |
| 俁俈 | 傛偟丂偝傫 | 2003/5/15丂0:02 | 搶嫗搒丂 |
| 俁俉 | damoto丂偝傫 | 2003/5/18丂13:53 | 撲偺拞1偱偡丂 |
| 俁俋 | 傎偘丂偝傫 | 2003/5/20丂13:59 | 杒偺塀傟壠 |
| 係侽 | ponta55555丂偝傫 | 2003/5/23丂19:12 | 丂 |
| 係侾 | hakase丂偝傫 | 2003/5/25丂15:58 | 峀搰丗旜摴 夛幮堳丂 |
| 係俀 | CRYING DOLPHIN丂偝傫 | 2003/5/25丂23:11 | 丂 |
| 係俁 | 嶼悢偺怷丂偝傫 | 2003/5/28丂15:06 | 丂 |
| 係係 | mhayashi丂偝傫 | 2003/5/31丂22:48 | 戝嶃晎丂 |
摎偊偼侾侽們倣偱偟偨丅
宖帵斅傛傝埲壓偺傛偆側夝偒曽傪捀偒傑偟偨丅
柺愊斾偲慄暘斾 丂亙ponta55555丂偝傫亜 - 2003/05/23 19:10 -
CD偲BA傪墑挿偟偰丄岎揰傪E偲偟丄
仮EAD=侾偲偟偰仮EBC亖係俋
偁偲偼柺愊偑俀係偢偮偵暘偗丄柺愊斾偐傜慄暘斾偵傕偳偟傑偟偨
丂
41 柺愊斾偺嬱巊 丂亙damoto丂偝傫亜 - 2003/05/18 15:04 -
AB偲CD傪墑挿偟偰丄岎揰傪O偲偡傞丅
AC:BD偑1丗7側偺偱丄嶰妏宍OAC:戜宍ABDC偼1丗48丅
戜宍ABDC偼丄慄暘mn偵傛偭偰丄戜宍ACnm丗戜宍mnDB偑1丗1偵側傞傛偆偵暘偗傜傟偰偄傞丅
亪嶰妏宍Omn:嶰妏宍OBD偼25丗49偲側傝丄倣n丗BD偼5丗7偲暘偐傞丅
傛偭偰丄mn偼10偲暘偐傞丅
僷僜僐儞巒傔偨偽偐傝偱丄僀僐乕儖側偳偺弌偟曽偑暘偐傝傑偣傫偱偟偨丅撉傒偵偔偐偭偨傜偛傔傫側偝偄丅
丂
40 俀忔偺暯嬒丂丂亙 僗僥僢僾丂偽偄丂僗僥僢僾丂偝傫亜
- 2003/05/06 18:51 -
偩偭偨傫偱偡偹丅
teki偝傫(#39)傪尒偰擺摼丅
AB丆CD偺墑挿偺岎揰傪P偲偟偰
仮PAD佷仮Pmn佷仮PBC
忦審傛傝
丂仮Pmn亖乮仮PAD亄仮PBC 乯/俀
偟偨偑偭偰
丂丂mn丱2亖乮AD丱2亄BC丱2乯/俀
丂丂丂丂丂亖侾侽丱2
傛偭偰
丂丂mn亖侾侽乮們倣乯丒丒丒摎偊
丂
39 俀忔偺斾 亙teki丂偝傫亜 - 2003/05/01 23:01 -
柺愊斾偑慄暘斾偺俀忔偵側傞偙偲偐傜
俀偺俀忔偲侾係偺俀忔乮亖侾俋俇乯偺暯嬒偱偡偹丅
傛偭偰丄併乮乮係+侾俋俇乯/俀乯亖併侾侽侽亖侾侽
偑摎偊偱偡丅
丂
38 柺愊斾傪憡帡斾偲傗偭偰丂亙 桳柍憡惗丂偝傫亜 - 2003/05/01 22:18 -
柺愊斾傪憡帡斾偲傗偭偰丄8們倣傪憲偭偰偄傑偟偨丅
柺愊偼摍偟偔側傞偼偢側偄偺偵丅
憡帡斾偺俀忔偱偟偨丅
俀摍暘偝傟傞柺愊傪俽丄BA偺墑挿偲俠俢偺墑挿偺岎揰傪俤偲偡傞偲丄
嶰妏宍俤俙俢偺柺愊傪俽乫偲偟傑偡丅
7*7丗1*1亖乮2S+S'):S'
傛傝俽亖24俽乫
mn=x偲偡傞偲丄
x*x:2*2=(S+S'):S'
傛傝丄(x/2)**2=(S+S')/S'=25
x/2=5偱x=10
丂
37 夝偗傑偟偨丅 亙kasama丂偝傫亜 - 2003/05/01 20:32 -
朸僒僀僩偱椶戣傪夝偄偨婥偑偟傑偡偑丄師偺傛偆偵峫偊傑偟偨丅恾偺傛偆側戜宍偱偼丄崅偝偼丄忋掙偲壓掙偲壗傜偐偺堦師娭學乮慄宍乯偵偁傝傑偡乮斾偲峫偊偰傕椙偄偲巚偄傑偡乯丅偮傑傝丄揔摉側幚悢倠偑懚嵼偟偰丄
丂戜宍偺崅偝亖倠丒忋掙亅倠丒壓掙亖倠乮忋掙亅壓掙乯
偲昞尰偱偒傑偡乮側偍丄忋掙偲壓掙偼媡偵偟偰傕堦斒惈傪幐偄傑偣傫乯丅慄暘倣値偺挿偝傪倵偲偡傞偲丄
丂忋偺戜宍偺柺愊亖(w+2)(w-2)k/2
丂壓偺戜宍偺柺愊亖(w+14)*(14-w)k/2
偱偡丅偙傟傪夝偔偲丄倵亖侾侽偲側傝傑偡丅
丂
36 俆寧崋丄抧摴偵夝偒傑偟偨 亙makisen丂丂偝傫亜 - 2003/05/01 01:48 -
晛捠偵倣値亖倶偲偍偄偰寁嶼偟傑偟偨丅
戜宍偺忋掙壓掙偺崌寁偺挿偝偺斾偑偍偗傞偺偱丄偍偺偍偺偺崅偝傕斾偱抲偗傑偡丅
俙倣値俢偺崅偝丄倠乮倶亅俀乯
倣俛俠値偺崅偝丄倠乮侾係亅倶乯
偁偲偼偦傟偧傟偺戜宍偺柺愊傪倶傪巊偭偰昞偟丄曽掱幃偲偟偰夝偔丄埲忋偱偡丅
http://www.ktplan.net/makisengogo/index.html
35 側傞傎偳 亙崅揷廋惉丂偝傫亜 - 2003/05/01 00:38 -
偝傜偵廲偵敿暘偵暘偗傟偽丆侾丗俀俆偱娙扨偵弌棃傑偡偹丅
偪側傒偵巹偼丆寁嶼偑柺搢偵側傝偦偆偩偨偺偱丆僄僋僙儖傪巊偄傑偟偨丅(~_~;)
http://homepage2.nifty.com/stkg/
34 憡帡斾仺柺愊斾 亙嵅摗 峀愰丂偝傫亜 - 2003/05/01 00:21 -
椶戣傪夁嫀偵宱尡偟偰偍傝丆偡偖摎偊偑傢偐傝傑偟偨丅
AB丆CD偺墑挿偺岎揰傪P偲偟偰
仮PAD佷仮Pmn佷仮PBC
憡帡斾丂2丗x丗14
柺愊斾丂4丗x丱2丗196
忦審傛傝
x丱2亅4亖196亅x丱2
x丱2亖100傛傝
x亖10
偦偺懠師偺傛偆側夞摎傪捀偒傑偟偨丅
亙傛偟丂偝傫亜
戜宍偺崅偝傪倛們倣偲偡傞
傑偨慄暘俙倣丗慄暘倣俛亖慄暘俢値丗慄暘値俠亖倠丗乮侾亅俲乯 乮侽
亝倠亝侾乯偲偡傞偲
慄暘倣値偺挿偝偼俀亄侾俀倠偲昞偣傞
崱丄戜宍俙倣値俢偲戜宍倣俛俠値偺柺愊偑摍偟偔側傞偲偄偆忦審偐傜
乮俀亄侾俀倠亄俀乯亊倠亊倛亖乮侾係亄侾俀倠亄俀乯亊乮侾亅倠乯亊倛
偙傟偼倠偵娭偡傞俀師曽掱幃偲側傞偺偱丄偙傟傪夝偄偰
倠亖亅侾丄俀乛俁
侽亝倠亝侾側偺偱 倠亖俀乛俁
傛偭偰
慄暘倣値亖俀亄侾俀亊俀乛俁亖侾侽乮們倣乯
亙埨妝丂偝傫亜
傑偢惵怓戜宍偺崅偝傪倣噋丄墿怓戜宍偺崅偝傪値噋偲偍偔偲
媮傔傞挿偝偼乮俀値亄侾係倣乯/乮値亄倣乯偲偐偗傞
戜宍柺愊偑乮忋掙亄壓掙乯仏崅偝亐俀偲側傞岞幃傪巊偆偲
戣堄偺忦審偐傜師偺摍幃偑偱偒傞丅
乷乮俀亄侾係乯仏乮倣亄値乯亐俀乸亐俀亖乮俀亄乮俀値亄侾係倣乯/
乮値亄倣乯乯仏倣亐俀
偙傟傪娙扨偵偡傞偲乮俀倣亄値乯仏乮倣亅俀値乯亖侽
傕偪傠傫倣丄値偼惓側偺偱倣亖俀値
偙傟偐傜媮傔傞挿偝俀値亄侾係倣乯/乮値亄倣乯傊戙擖偟偰
侾侽僙儞僠偑偱傑偡
亙屵擭偺偆傝傏偆丂偝傫亜
捈慄俙俛偲捈慄俠俢偲偺岎揰傪俹偲偟偰丄仮俹俙俢丄戜宍俙倣値俢丄戜
宍倣俛俠値偺柺愊傪偦傟偧傟倳丄倴丄倴丄倣値亖倶乮亜侽乯偲偡傞偲丄
嶰妏宍偺憡帡傛傝丄
倳乛乮倳亄俀倴乯亖侾乛係俋丆倳乛乮倳亄倴乯亖係乛乮倶丱俀乯丆
乮倳亄倴乯乛乮倳亄俀倴乯亖乮倶丱俀乯乛侾俋俇
亪倶亖侾侽乮們倣乯乧乮摎乯
亙MARORINE丂偝傫亜
夝愢丗捀揰俢偐傜曈俙俛偵暯峴側曗彆慄傪堷偒丆倣値偲偺岎揰傪俤丆
丂丂丂俛俠偲偺岎揰傪俥偲偡傞丅偙偙偱丆倣値亖冊們倣偲偡傞偲丆
丂丂丂巐妏宍俙倣俤俢丆俙俛俥俢偼暯峴巐曈宍偲側傞偺偱丆
丂丂丂倣俤亖俛俥亖俀們倣丆俤値亖乮冊亅俀乯們倣丆俥俠亖侾俀們倣丏
丂丂丂俤値//俥俠傛傝丆仮俢俤値佷仮俢俥俠丆俢値丗俢俠亖俤値丗俥俠
丂丂丂亖乮冊亅俀乯丗侾俀丆
丂丂丂傛偭偰丆俢値丗値俠亖乮冊亅俀乯丗乮侾係亅冊乯
丂丂丂偟偨偑偭偰丆戜宍俙倣値俢亖戜宍俛倣値俠傛傝丆
丂丂丂乮冊亄俀乯亊乮冊亅俀乯亐俀亖乮侾係亄冊乯亊乮侾係亅冊乯亐俀
丂丂丂俀冊2亖俀侽侽丆冊2亖侾侽侽丆冊亜侽傛傝丆冊亖侾侽乮們倣乯
亙昹揷柧枻偝傫亜
倁倝倱倳倎倢丂Basic偱夝愅偟偰偄偨偩偒丄mn=9.9999999999993們倣偲夝愅偟偰偄偨偩偒傑偟偨丅
僜乕僗僾儘僌儔儉偑昁梫側曽偼丄偍抦傜偣偔偩偝偄丅
丂
丂
丂