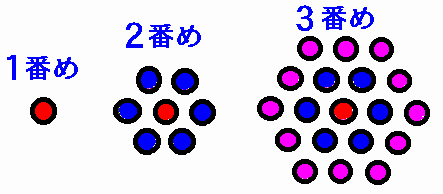
1番目は一本であり、2番めでは7本であり、3番目では19本になります。
瀬戸大橋では、細い鋼鉄線が10番目まで束ねられているようです。
ここで問題です。束ねてある鋼鉄線は何本になるでしょうか。
「

|
|
上図を見て下さい。内部をうめる6角数を、有心六角数というそうです。これは、同じ太さののロープを縛って固定するときに、最も安定した状態にできる数になるようです。 1番目は一本であり、2番めでは7本であり、3番目では19本になります。 瀬戸大橋では、細い鋼鉄線が10番目まで束ねられているようです。 ここで問題です。束ねてある鋼鉄線は何本になるでしょうか。 |
<正解者一覧表>
| 正解者順位 | name | メール到着日時 | 備 考 |
| 1 | 高田修成(修徳学院) さん | 2003/6/1 0:01 | 兵庫県 |
| 2 | 午年のうりぼう さん | 2003/6/1 0:04 | 福島県 |
| 3 | 信三 さん | 2003/6/1 0:04 | シリコンバレーの住人 |
| 4 | nobu さん | 2003/6/1 0:05 | 石川県 |
| 5 | ささ さん | 2003/6/1 0:05 | |
| 6 | ろろ さん | 2003/6/1 0:06 | 神奈川県 |
| 7 | teki さん | 2003/6/1 0:06 | |
| 8 | 算数の森 さん | 2003/6/1 0:06 | 兵庫県 |
| 9 | テモ さん | 2003/6/1 0:07 | 広島市の美鈴が丘 |
| 10 | isami さん | 2003/6/1 0:08 | 高知県 会社員 |
| 11 | 呑 さん | 2003/6/1 0:12 | |
| 12 | 経友会の進作 さん | 2003/6/1 0:13 | 京都府木津町・64歳 |
| 13 | mhayashi さん | 2003/6/1 0:15 | 大阪府 |
| 14 | 桂おとこ さん | 2003/6/1 0:21 | |
| 15 | 佐藤 広宣 さん | 2003/6/1 0:23 | 東京都 |
| 16 | ささ さん | 2003/6/1 0:27 | |
| 17 | Nの悲劇 さん | 2003/6/1 0:35 | 兵庫県 |
| 18 | すてっぷ さん | 2003/6/1 0:42 | 気分はいつでも中学生 |
| 19 | 土居 千珠 さん | 2003/6/1 0:50 | 愛媛県 中一 |
| 20 | miya さん | 2003/6/1 0:52 | 熊本 |
| 21 | Michael さん | 2003/6/1 1:39 | |
| 22 | モルモット大臣 さん | 2003/6/1 8:36 | モルモット王国 |
| 23 | みちこ さん | 2003/6/1 10:11 | |
| 24 | なにわ さん | 2003/6/1 10:35 | 西宮市 |
| 25 | 巷の夢 さん | 2003/6/1 14:59 | 宮城県出身 |
| 26 | 有無相生 さん | 2003/6/1 18:30 | 会社員、神奈川県 |
| 27 | 颯馬 さん | 2003/6/1 19:37 | |
| 28 | 安楽 さん | 2003/6/1 22:37 | 宮崎県小林市 |
| 29 | フィリピンの鷹 さん | 2003/6/2 0:49 | フィリピン在住39歳 |
| 30 | MARORINE さん | 2003/6/2 1:19 | 福岡県在住、某進学塾講師 |
| 31 | kasama さん | 2003/6/2 18:17 | 和歌山県プログラマ |
| 32 | 元先生の教え子 さん | 2003/6/2 19:24 | 兵庫県の高校生 |
| 33 | ψ(プサイ) さん | 2003/6/3 2:50 | 小学生気分の抜けない中一です |
| 34 | TOMOAKI さん | 2003/6/3 16:15 | 大分県 |
| 35 | Banyanyan さん | 2003/6/4 3:10 | 京都府 |
| 36 | yu さん | 2003/6/4 16:07 | |
| 37 | 浜田明巳 さん | 2003/6/7 13:22 | |
| 38 | yuki さん | 2003/6/7 16:07 | 奈良県 |
| 39 | ISAMU さん | 2003/6/8 15:23 | 三重県 |
| 40 | 清川 育男 さん | 2003/6/9 0:33 | 広島市 |
| 41 | あごら みのる さん | 2003/6/9 16:38 | 福岡県 |
| 42 | damoto さん | 2003/6/11 1:06 | 兵庫県の中学生です |
| 43 | ほげ さん | 2003/6/11 12:14 | 北の隠れ家 |
| 44 | しおり さん | 2003/6/14 19:39 | |
| 45 | 阿久根光 さん | 2003/6/18 21:47 | 小4です |
| 46 | スモークマン さん | 2003/6/22 14:34 | 生息地 金光 |
| 47 | ピカピカの中学二年生 さん | 2003/6/23 17:23 | 神戸市 |
| 48 | にゃじら さん | 2003/6/24 0:07 | にゃじら |
| 49 | あつきパパ さん | 2003/6/24 11:31 | あいち |
| 50 | ふじさきたつみ さん | 2003/6/25 20:51 | 北海道 |
答えは、271本です。
<掲示板より>
<Banyanyan さん> - 2003/06/04 03:13 -
1周目 1
2周目 1×6
3周目 2×6
・・・
10周目 9×6
1+(1+2+・・・+9)×6
=1+45×6
=271
< 規則性 kasama さん> - 2003/06/02 18:15 -
一番外側の鋼鉄線の本数は
1番目 1
2番目 6
3番目 12
・・・
n番目 6(n-1)
と推側されるので、n番目まで束ねると
n
Σ{6(i-1)} + 1 = 3n(n-1) + 1 (ただし、n > 1)
i=10
となり、n=10を代入してすると答えが得られます。
< 本当は地道に数えました… MARORINE さん> - 2003/06/02 01:14 -
【解答】271本
【解説】1番目…1(本)、2番目…1+6(本)、3番目…1+6+ 12(本)、4番目…1+6+12+18(本)、5番目… 1+6+12+18+24(本)より、
n番目の本数は、
{6+6(n−1)}×(n−1)÷2+1(本)で表される。
よって、n=10より、{6+6(10−1)}×(10−1) ÷2+1=271(本)
<49 やれやれ WAT さん> - 2003/06/02 00:56 -
1周りで6本づつ増えていく
<48 階差数列 有無相生 さん> - 2003/06/01 18:29 -
n番目の周辺の個数は、6*n-6で、
n番目の中身を含めた個数をp(n)とすると、
p(n+1)-p(n)=6*(n-1)
n=1,...,(n-1)を代入して、辺辺を揃えて足すと、
p(n)-p(1)=6*[1+2+...+(n-1)]=3*(n-1)*n
p(n)=p(1)+3*(n-1)*n=1+3*(n-1)*n
p(10)=271
<47 規則性を使った問題でした♪ みちこ さん> - 2003/06/01 18:15 -
1(真ん中の1本)+2(番目)×6(六角形だから)−6(重なっている部分)+3(番目)×6−6+・・・・・・・・としていくと、結局1+6+12+18+24+30+36+42+48+54=271になりました。
<46 階差数列 午年のうりぼう さん> - 2003/06/01 00:15 -
求めるものをa(10)とおく。
a(10)−1=シグマ(n=1〜9)6n
=270
∴a(10)=271
<45 1 + 6×Σ9 teki さん> - 2003/06/01 00:11 -
周囲の鋼鉄線の本数の規則性がわかれば、解けますね。
2番目以降は、6本ずつ増えていくことから、6+12+18+24+・・
=6×Σ9となります。
これに、最初の1本を足して、271本ですね。
その他 メールより
<ふじさきたつみ さんより>
真ん中の一本をのぞいて、6つの三角形にわけてかぞえると
6×Σ9+1=6×45+1=271
<あつきパパ さんより>
一本目が1
二本目が2+3+2
三本目が3+4+5+4+3
・・・
十本目は10+11+12+13+14+15+16+17+18+1
9+18+17+16+15+14+13+12+11+10=271
本?
<にゃじら さんより>
(1+2+3+4+5+6+7+8+9)*6+1=271
<スモークマン さんより>
(10+9+8+7+6+5+4+3+2) x 6 - 9 x 6 + 1 =(54-9)x6+1=271
<yuki さんより>
10×11÷2×6-10×6+1=271
<浜田 明巳さんより>
n番目にf(n)本あるとすると,漸化式
f(n+1)=f(n)+6n,f(1)=1
が成り立つ.
故にn>1のとき,
f(n)=f(1)+Σ(1≦k≦n-1) {f(n+1)−f(n)}
=1+Σ(1≦k≦n-1) 6k
=1+6×(n−1)n/2
=3n^2−3n+1
これはn=1のときも成立する.
∴f(n)=3n^2−3n+1
∴f(19)=3×19^2−3×19+1=1027
エクセルのマクロ
Option Explicit
Sub Macro1()
Sheets("Sheet1").Select
Dim n As Integer
Cells(1, 1).Value = 1
For n = 2 To 19
Cells(n, 1).Value = Cells(n - 1, 1).Value + (n -
1) * 6
Range("A" & Right(Str(n), Len(Str(n))
- 1)).Select
Next n
End Sub
<MARORINE さんより>
【解説】1番目…1(本)、2番目…1+6(本)、3番目…1+6+
12(本)、4番目…1+6+12+18(本)、5番目…1+6+1
2+18+24(本)より、n番目の本数は、{6+6(n−1)}×
(n−1)÷2+1(本)で表される。よって、n=10より、{6+6
(10−1)}×(10−1)÷2+1=271(本)
<安楽 さん>
等差数列なので、一般項an=3*n^2-3n+1を求める
<teki さん>
解法 1番目:1本 2番目:6×1本 3番目:6×2本 ・
・ ・ 10番目:6×9本 となることから、総本数は、1+6×Σ9=1+6×45=271