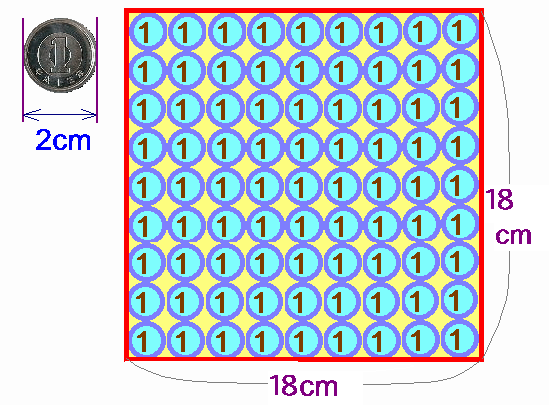
ここで問題です。上手く並べ替えるとこの額の中に最高何円並べることが出来るでしょうか。 (ただし、一円玉どおしは、重ならないようにします。)
「

|
|
上図を見て下さい。直径2cmの一円玉を一辺が18cmの正方形の額の中に規則正しく並べています。一円玉は全部で81円並べられています。 ここで問題です。上手く並べ替えるとこの額の中に最高何円並べることが出来るでしょうか。 (ただし、一円玉どおしは、重ならないようにします。) |
<正解者一覧表>
| 正解者順位 | name | メール到着日時 | 備 考 |
| 1 | フィリピンの鷹 さん | 2003/7/1 0:19 | フィリピン在住39歳 |
| 2 | 高田修成(修徳学院) さん | 2003/7/1 0:56 | 兵庫県揖保郡 |
| 3 | ろろ さん | 2003/7/1 6:41 | 神奈川県 |
| 4 | 信三 さん | 2003/7/1 7:54 | シリコンバレーの住人 |
| 5 | nobu さん | 2003/7/1 8:00 | |
| 6 | 午年のうりぼう さん | 2003/7/1 9:29 | 福島県 |
| 7 | 佐藤 広宣 さん | 2003/7/1 11:22 | |
| 8 | Michael さん | 2003/7/1 12:10 | |
| 9 | teki さん | 2003/7/1 13:44 | |
| 10 | 土居 千珠 さん | 2003/7/1 14:31 | 愛媛県、中一 |
| 11 | 呑 さん | 2003/7/1 15:16 | |
| 12 | kasama さん | 2003/7/1 16:02 | 和歌山県プログラマ |
| 13 | miya さん | 2003/7/1 17:26 | 熊本 |
| 14 | BB さん | 2003/7/1 18:54 | 東京都 |
| 15 | なにわ さん | 2003/7/1 20:04 | 西宮市 |
| 16 | 桂おとこ さん | 2003/7/1 22:52 | こてこての大阪人 |
| 17 | 奥入瀬 さん | 2003/7/2 1:23 | 東京 |
| 18 | 巷の夢 さん | 2003/7/2 7:18 | 宮城県出身 |
| 19 | 経友会の進作 さん | 2003/7/2 7:46 | 京都府木津町・65歳 |
| 20 | みかん さん | 2003/7/2 13:01 | 神奈川県・高校生 |
| 21 | 勇水 さん | 2003/7/3 22:25 | 高知県香美郡 |
| 22 | あみ〜ご さん | 2003/7/6 0:42 | |
| 23 | テモ さん | 2003/7/6 15:24 | 広島市の美鈴が丘 |
| 24 | POPPY さん | 2003/7/8 0:43 | 東京都 |
| 25 | 高橋 道広 さん | 2003/7/13 11:30 | 北の隠れ家 |
| 26 | yuki さん | 2003/7/17 1:29 | 奈良県 |
| 27 | HK さん | 2003/7/19 8:02 | 富山市寺町 自営業 |
| 28 | banyanyan さん | 2003/7/21 13:53 | 京都府 |
| 29 | 永弘 世之介 さん | 2003/7/21 22:35 | 東京都 |
| 30 | ビッキー さん | 2003/7/23 23:56 | 名古屋市 |
答えは86円でした。
実際に一円玉を並べてみました。

掲示板に非常に楽しい書き込みをしていただきました。
68 re:意外と入るなあ よしおか(管理人) -
2003/07/03 18:46 -
面白く読みました。私の職場でこの話をすると、感心しておられました。
そこで、何枚はいるか計算しました。1円玉の厚さは、約1.51mmです。
この値で計算すると、この正方形の中に、1072枚も入ることが分かりました。
65 意外と入るなあ みかん - 2003/07/02 12:47 -
はじめは私も85個だろうと思っていたのですが、認証ではねられました。ではあと1個入るのだろうなあ、と思いつつもでたらめ入れて正解したというのは何か癪に障るので端の段にもう一個入れられないかと試しました。するともう一個入ってめでたし、となりました。
ところで学校でこの問題を友人に話したところ、重ねてはいけないという条件なのだから一円玉を立てて並べるのはどうだ、という人がいました。一円玉の厚みはよくわからないけれど86個の数倍は並べられると思うのですがさすがにそれは「数学」の問題としてはなしですよね。
63 当面はこの数字まで・・・ 経友会の進作 - 2003/07/02 07:38
-
先月末で65歳となりました。いよいよ「老人人口」の
仲間入り。今回の問題は数字の連続性というものを逆手に
とって「人間の単純性」をあざ笑うかのごときものでした。
答は86。当面は86歳まで、算数問題を解きたいですね。
62 落とし穴に1円玉があった…って感じ! MARORINE -
2003/07/02 03:04 -
単純に考えすぎました。規則の中にも変則があるとは…。でも、無事に解決してホッと一息…。
60 実は teki - 2003/07/01 19:33 -
高橋道広さんのHP「みっちの隠れ家」の数学の問題第7問に同様の
問題があり、以前に解いてましたので、すぐに分かりました。
もっと、難しいのは同じHPの投稿問題でCD(Crying Dolphin)
さんが出した問題です。
興味のある方は、下記のアドレスの「過去問」の欄を見てください。
http://micci.sansu.org/
59 あと一つ置けたのか・・・ kasama - 2003/07/01 16:11 -
直感的に9個、8個、9個、・・・という具合に1円玉を列方向に交互にずらして並べると良さそうなので・・・
n列並べたときの幅の合計が18以下となれば良いので 2+(n-1)√3
< 18 → n < 10.2 となり、10個並べることができますね^-^;つまり、
9+8 + 9+8 + 9+8 + 9+8 + 9+8 = 85
と思ったが・・・認証で蹴られました~~;よく考えてみると、最終列にもう1個置くことができたんですね^-^;
58 実は フィリピンの鷹 - 2003/07/01 13:36 -
以前類似問題を解いたことがあって、詰めなおすと7列のスペースに
8列並ぶ事を知っていたので、早く出来ました。
81+8−3=86
57 あつきパパ あつきパパ - 2003/07/01 12:08 -
半径1の円 X^2+Y^2=1・・? (X-2)^2+Y~2=1・・? このとき??の両方の円に接する半径1の円・・?を考える。
?の円の中心は、???の中心を結ぶと正三角形を作ることを
考えるとY=tan60°X上にあり、X座標は??2円の中点の1である。
よって?の中心は(1,√3)である。
以上のことを鑑みて、(座標系はここから別) (0,0),(18,18)間に半径1の円を並べてみると 下から1列目Yが0から2の範囲に9つの円を並べることができる。 下から2列目Yが√3から√3+2の範囲に8つの円を並べることができる。 下から3列目Yが2√3から2√3+2の範囲に9つの円を並べることができる。 これを一般化すると a列目Yが√3(a-1)から√3(a-1)+2の範囲に並べることができる、となる。 よって、√3(a-1)+2≦18より a≦10.2より10列目まで並べることができる。 また下から奇数列目は9つの円を、偶数列目は8つの円を並べることができるから 但し、9列目のY座標は13.85から15.85までなので、10列目に2以上の余裕ができるから、 10列目は偶数目でも9つの円を並べることができる。 よって、9*6+8*4=86円
http://homepage2.nifty.com/yopida/
55 何度も間違えてごめんなさい。 ろろ - 2003/07/01 06:53 -
でも、どうしても86になっちゃうんです。
9段まで積むと高さが 2+8√3≒15.9
すると、あと隙間が18−15.9=2.1cmできて
最後の段には9個入ると思うんです。
9+8+9+8+9+8+9+8+9+9=86
だめですか? まだ、寝ぼけているかも
http://www1.ttcn.ne.jp/~roro/
その他メールで頂きました。
<ビッキー さん>
9個の列5と8個の列4の幅を計算すると、3枚の1円で出来る正三
角形の高さから√3×8+2≒15.8cmとなる。更に18−15.8=2.2で1円
が9×1列入る。
<テモ さん>
直感で9,8,9,8,9,8,9,8,9となって4個少ないが最後
に1列入るので結局増える。9個入るか列の幅を計算したら2cmを超え
るので、9個入り合計86個
<BB さん>
円の中心同士を結ぶ図形が正方形を形成する場合(問題の初期状態)、
単位面積あたりの円の占有率は約78%なのに対し、円の中心同士を結
ぶ図形が正三角形を形成する場合、単位面積あたりの円の占有率は9
0%超に達するため、できる限り円の中心同士を結ぶ図形が正三角形に
なるような並べ方を繰り返すのが効率がよい。
3つの円の中心が作る正三角形は1辺が2cm
底辺を額の底辺と平行に並べると高さがsqrt(3)cm
9つの円を額の底辺に沿って並べる場合の円の中心が、
底辺16cm、高さ8*sqrt(3)cmの正三角形を成すように並べると、
底辺から、9円,8円,9円,8円,9円,8円,9円,8円,9円の77円が並ぶ。
さらに上部に2cm以上の隙間があるので、9円を並べることができる。
以上で、合計77円+9円の86円
<teki さん>
1円玉の並べ方として最大になるのは、1段目から順に交互に積む並べ方で、
9、8、9、8、9、8、9、8、9、9の合計86枚が最大です。
交互に並べると高さが2ではなく、1+√3/2になる