「今月の問題」　第４９回　（平成１５年１０月）

　
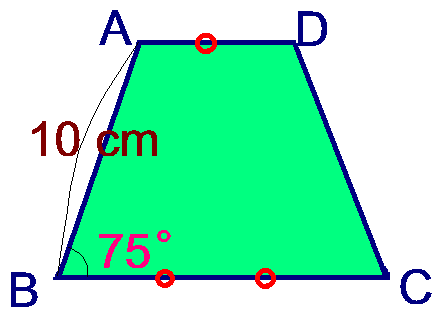
上図の等脚台形ＡＢＣＤがあります。
この台形は、ＢＣ＝２ＡＤ　であり、ＡＢとＣＤの長さは１０ｃｍであることが分かっています。
また、∠ABCの大きさは、ちょうど７５度になっています。
　
ここで問題です。この台形ＡＢＣＤの面積は、何ｃｍ２でしょうか。　

＜正解者一覧表＞　 　　　　　　　　　　　
正解者順位 　　　　ｎａｍｅ　　　 　　メール到着日時　　 　　備　考　　
　１佐藤 広宣　さん2003/10/1　0:00　
　２ 高田修成(修徳学院)　さん2003/10/1　0:02兵庫県揖保郡
　３ CRYING DOLPHIN　さん2003/10/1　0:06高知県？
　４nobu　さん2003/10/1　0:09石川県
　５kasama　さん2003/10/1　0:11和歌山県プログラマ　
　６桂おとこ　さん2003/10/1　0:11　
　７teki　さん2003/10/1　0:11大阪府
　８Michael　さん2003/10/1　0:12　
　９山羊　さん2003/10/1　0:14大阪
１０カバシン　さん2003/10/1　0:16福岡大学生
１１Nの悲劇　さん2003/10/1　0:17兵庫県・神戸市
１２モルモット大臣　さん2003/10/1　1:04モルモット王国　
１３信三　さん2003/10/1　1:17シリコンバレーの住人　
１４奥入瀬　さん2003/10/1　1:20東京都　
１５ 算数の森　さん2003/10/1　2:20兵庫県
１６ ろろ　さん2003/10/1　2:59神奈川県
１７miya　さん2003/10/1　4:42　
１８巷の夢　さん2003/10/1　7:05宮城県出身
１９ 呑　さん2003/10/1　10:18ただいま療養中
２０ BONZ　さん2003/10/1　13:09大阪市
２１みかん　さん2003/10/1　18:32神奈川県
２２ 有無相生　さん2003/10/1　19:28神奈川県、会社員
２３あみ〜ご　さん2003/10/1　20:24　
２４なにわ　さん2003/10/1　21:26　
２５午年のうりぼう　さん2003/10/1　21:28　
２６すてっぷ　さん2003/10/2　11:22いつも・やっとこ・さっとこ　
２７浜田　明巳　さん2003/10/2　11:30　
２８ビッキー　さん2003/10/2　16:16名古屋市　
２９数学大好き大輔　さん2003/10/2　20:43兵庫県出身　
３０ちず　さん2003/10/2　21:39愛媛県　
３１およよ　さん2003/10/2　20:43兵庫県出身　
３２yan　さん2003/10/3　7:17　
３３pooh　さん2003/10/3　16:32大阪府　　
３４雨夜の品定め　さん2003/10/3　22:28徳島市　
３５テモ　さん2003/10/3　22:23広島市の美鈴が丘　
３６安楽　さん2003/10/4　14:31　
３７zizi　さん2003/10/4　14:38東京都・ふつうのお○さん　
３８ mm-labo　さん2003/10/4　23:47　
３９経友会の進作　さん2003/10/5　17:32京都府木津町・６５歳
４０ken　さん2003/10/5　21:51　
４１maki　さん2003/10/6　1:45兵庫県　
４２あめま　さん2003/10/6　12:53滋賀県　
４３ あつきパパ　さん2003/10/6　14:23０歳児の父
４４隆幸40歳　さん2003/10/7　12:36広島県福山市　
４５フィリピンの鷹　さん2003/10/7　16:04フィリピン在住　
４６なおぽん　さん2003/10/7　22:23京都府　
４７neo　さん2003/10/8　6:29　
４８JIRO　さん2003/10/8　16:52兵庫県豊岡市　
４９isami　さん2003/10/9　23:34高知県土佐山田町　
５０永弘 世之介　さん2003/10/10 13:01東京都　
５１ 高橋　道広　さん2003/10/11 7:46北の隠れ家
５２MARORINE　さん2003/10/13 12:01福岡県在住、某進学塾講師　
５３離宮　さん2003/10/17 23:02　
５４ カロビー生涯学習講座・数学コース　さん2003/10/20 19:13　
５５Ｈ・Ｋ　さん2003/10/21 18:08富山市寺町　自営
５６トド３号　さん2003/10/25 22:38静岡県
５７taichi　さん2003/10/26 22:16山形県
５８ きょろ文　さん2003/10/27 18:44　
５９東京学館浦安高校　さん2003/10/28 23:13千葉県在住
６０ mhayashi　さん2003/10/31 23:59大阪府　

こたえは、７５ｃｍ２でした。

次のような回答を皆さんより頂きました。有難うございます。

＜東京学館浦安高校　さん＞
 ＡＢ、ＣＤの延長上の交点をＥとすると、角ＢＥＣ＝３０°、Ｅ
Ｂ＝ＥＣ＝２０なので、三角形ＥＢＣの面積は２０×２０×sin３
０°になる。また、台形ＡＢＣＤはこの三角形の４分の３だから
計算するとその面積は７５になる。

＜MARORINE　さん＞
【解説】ＡからＤＣに平行な線を引き，ＢＣとの交点をＥとすると，△
ＡＢＥはＡＢ＝ＡＥ＝10cm，頂角30°の二等辺三角形となる。ここで，
ＢからＡＥに対して垂線ＢＨを引くと，△ＡＢＨは90°，60°，30°の
直角三角形であるから，ＢＨ＝10÷2＝5cm，よって，△ＡＢＥ＝10×5
÷2＝25cm2となり，求める台形の面積はこの三角形３つ分にあたるか
ら，台形ＡＢＣＤ＝25×3＝75cm2となる。

＜なおぽん　さん＞
平行四辺形を作りさらに対角線を引くと、図の台形は底角７５度の
二等辺三角形が３つできる。頂角が３０度なのでそれを利用し、
１０センチの辺を底辺とすると高さは５センチとなり、三角形は
１０×５÷２＝２５　その３倍で７５

＜あつきパパ　さん＞
ＢＣの中点をＭとおくと、
△ＡＢＭと△ＤＣＭは合同（ＡＢ＝ＤＣ＝１０、ＢＭ＝ＣＭ、∠ＡＢＭ
＝∠ＤＣＭ＝７５°）
同様に△ＡＢＭと△ＭＤＡも合同（ＭＢ＝ＡＤ、ＡＭ＝ＭＡ、ＡＢ＝Ｍ
Ｄ＝１０（∵△ＡＢＭ＝ＤＣＭ））
以上から四角形ＡＢＣＤは合同な二等辺三角形３つによりできている。
ひとつの三角形の面積は、１０×１０×sin３０°÷２＝２５
よって、２５×３＝７５

＜mm-labo　さん＞
BCの中点をEとし、AE、DEを結びます。
すると、三角形が三つできますが、それは、全部二等辺三角形にな
ります。
これらは、全て等辺が10cmで頂角が30°の二等辺三角形になります。
したがって、例えば、三角形ABEの面積を考えて、それを三倍すれ
ばよいことになります。
ここで、Bから直線AEに向けて垂線を下ろし、その垂線をHとします。
すると、30°-60°-90°の直角三角形の性質から
BHは5cmになります。
よって、三角形ABEの面積 = (5*10)/2 = 25
これを三倍して求める面積は75(cm^2)となります

　

＜雨夜の品定め　さん＞
まず線分ＡＢをＡ方向に伸ばし、同様にＣＤもＤ方向へ伸ばします。
交点をＥとすると、∠ＡＥＤ＝３０°となる。
さらにＡＤ：ＢＣ＝１：２より中点連結定理が適用ＡＥ＝ＤＥ＝１０
次にＢから線分ＥＣに垂線を下ろし、交点をＦとします。すると
△ＢＥＦが30°60°90°の三角形となり三平方の定理よりＢＦ＝１０
ＥＣ＝２０，ＢＦ＝１０より２０＊１０＊１/２＝１００
これから△ＡＥＤの面積を引きます。
△ＡＥＤ：△ＢＥＣ＝１：３より１００＊３/４＝７５

∴台形ＡＢＣＤ＝７５cm~2

＜およよ　さん＞
線分BCを二等分する点Eに、点A・点Dから線を引
くと３つの等面積の三角形が出来ます。∠BAEが30度。点Bから線
分AEに直交する線を引き、交点をFとする。すると∠ABFは60度な
ので、線分BFの長さは5cm、AEは10cmなので、三角形ABEの面積は
25cm2。台形はこの三角形が３つくっついた形なので三角形の面積
を3倍して75cm2です


＜浜田　明巳さん＞
visual　basicを使ってプログラムで計算していただきました。そのプログラムを送っていただきましたが、
計算結果から７５cm2を示していただきました。
ちなみに、AD＝5.1763････ｃｍになり、BC＝10.3527・・・・になるようです。

＜午年のうりぼう　さん＞
 ＡＢとＤＣをそれぞれ延長して、二等辺三角形を作る。
ＡＢとＤＣのそれぞれの延長の交点をＥとすると、
中点連結定理より、ＢＥ＝ＣＥ＝２０（ｃｍ）
ＣからＢＥに下ろした垂線の足をＨとすると、
ＥＨ＝１０√３（ｃｍ）、ＣＨ＝１０（ｃｍ）
∴△ＣＥＨ＝５０√３（ｃｍ）
　△ＣＢＨ＝１００−５０√３（ｃｍ）（△ＣＥＨと△ＣＢＨとは高さ
が共通。）
∴△ＥＢＣ＝１００（ｃｍ）
∴台形ＡＢＣＤ＝（３／４）△ＥＢＣ＝７５（ｃｍ）

　

その他、正解者掲示板にも解き方等、親切に教えていただきました。有難うございました。