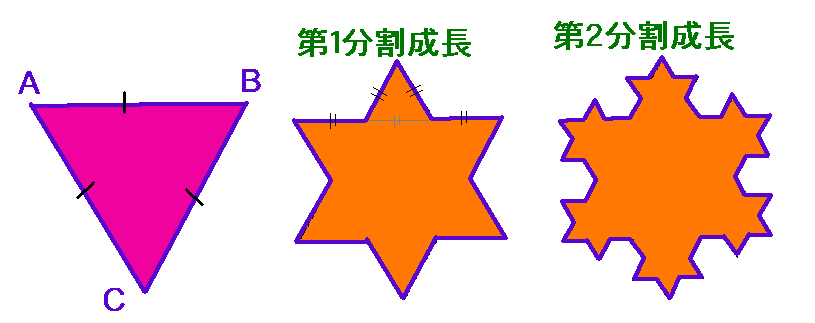
上図を見てください。
正三角形ABCがあります。この三辺をそれぞれ三等分します。
その三等分した辺一辺とする正三角形を書き加え、第1分割成長図を書きます。
同様にして、一番右は、第2分割成長図になります。
ここで問題です。分割を繰り返すと面積がふえますが、第3分割成長図は、元の正三角形ABCの面積の何倍になるでしょうか。
※答えは分数の形で答えてください
「

|
|
上図を見てください。 正三角形ABCがあります。この三辺をそれぞれ三等分します。 その三等分した辺一辺とする正三角形を書き加え、第1分割成長図を書きます。 同様にして、一番右は、第2分割成長図になります。 ※答えは分数の形で答えてください |
<正解者一覧表>
| 正解者順位 | name | メール到着日時 | 備 考 |
| 1 | 呑 さん | 2003/12/1 22:04 | |
| 2 | ろろ さん | 2003/12/1 22:04 | 神奈川県 |
| 3 | JIRO さん | 2003/12/1 22:12 | 兵庫県豊岡市 |
| 4 | neo さん | 2003/12/1 22:14 | |
| 5 | ゴンとも さん | 2003/12/1 22:15 | YMOチルドレン in 豊川市 |
| 6 | nobu さん | 2003/12/1 22:17 | 石川県 |
| 7 | フィリピンの鷹 さん | 2003/12/1 22:30 | フィリピン在住 |
| 8 | Michael さん | 2003/12/1 22:31 | |
| 9 | yan さん | 2003/12/1 22:31 | 愛知県 |
| 10 | なにわ さん | 2003/12/1 22:41 | 西宮市 |
| 11 | kasama さん | 2003/12/1 22:41 | |
| 12 | ちず さん | 2003/12/1 22:52 | 愛媛県 |
| 13 | 山羊 さん | 2003/12/1 23:16 | |
| 14 | 寺脇犬 さん | 2003/12/1 23:21 | 生駒市 |
| 15 | モルモット大臣 さん | 2003/12/1 23:28 | モルモット王国 |
| 16 | 勇水 さん | 2003/12/1 23:41 | 高知県土佐山田町 |
| 17 | 佐藤 広宣 さん | 2003/12/2 0:05 | |
| 18 | 算数の森 さん | 2003/12/2 0:24 | 兵庫県 |
| 19 | 奥入瀬 さん | 2003/12/2 2:06 | |
| 20 | miya さん | 2003/12/2 5:13 | |
| 21 | 信三 さん | 2003/12/2 5:28 | シリコンバレーの住人 |
| 22 | なか さん | 2003/12/2 7:31 | 北海道 |
| 23 | 経友会の進作 さん | 2003/12/2 8:12 | 京都府木津町・65歳 |
| 24 | teki さん | 2003/12/2 9:18 | 大阪府 |
| 25 | 元先生の教え子 さん | 2003/12/2 16:46 | 兵庫県某高校 |
| 26 | あつきパパ さん | 2003/12/3 10:48 | 愛知県 0歳児の父 |
| 27 | 安楽 さん | 2003/12/3 23:31 | 宮崎県小林市 |
| 28 | みかん さん | 2003/12/4 21:03 | 神奈川県 |
| 29 | 宮 さん | 2003/12/5 11:34 | 鹿児島県 予備校生 |
| 30 | zizi さん | 2003/12/7 21:15 | 東京都 |
| 31 | なおっち さん | 2003/12/7 21:16 | 佐賀県 |
| 32 | 巷の夢 さん | 2003/12/8 7:28 | 宮城県出身 |
| 33 | HK さん | 2003/12/9 17:16 | 富山市寺町 自営業 |
| 34 | Kodatan さん | 2003/12/12 18:58 | |
| 35 | 仮面X さん | 2003/12/21 18:58 | 中1です |
| 36 | 燕陣内 さん | 2003/12/24 12:08 | |
| 37 | mhayashi さん | 2003/12/31 20:46 | 大阪府 |
| 38 | すてっぷ さん | 2003/12/31 21:24 | |
答えは、376/243倍です
次のように正解者掲示板に書き込みを頂きました。
141 <この作業を> tekiさん - 2003/12/02 11:40 -
ずっと続けると、最終的には元の正三角形の面積の1.6倍の面積を
持つフラクタクル図形ができますね。
140 <ギャッと思ったが・・・>
経友会の進作さん - 2003/12/02 08:25 -
これはまたどんな問題かと一瞬身構えましたが、辺の数と
三角形の面積を追えばいいと分かり一安心。元の三角形の面
積を1と置いて(1)は1/9*3、(2)は1/81*12、(3)は1/729
*48、あわせて133/243が増加分。それに元の三角形を加えて
376/243。元の三角形を1と置いているので376/243が答え。
139 <計算間違えでつまづきました>:P LED さん - 2003/12/02
02:40 -
>個数
ひとつの辺につき、ひとつずつ正三角形が増える =>分割する前の辺の数=増える正三角形の数
分割すると、ひとつの辺が4つの辺になる(伝わりにくいなぁ
___ => _/\_
あとは、バーニィー・バーニィーさんと同じように解きました。
138 <出来てうれしい!>
バーニィー・バーニィーさん - 2003/12/02 02:26 -
一段階目の小さい正三角形は元の正三角形の1/9でそれが3個分増加。
二段階目の小さい正三角形は元の正三角形の1/9×1/9で、それが12個分増加。
三段階目の小さい正三角形は元の正三角形の1/9×1/9×1/9で、それが48個分増加。
つまり元の正三角形の面積をSとすれば、
S+3/9S+12/81S+48/729S=376/243S
以上、地道でした!
137 <3回間違えました。> ゴンともさん - 2003/12/01
23:23 -
簡単だといい第二段階を送り 40/27
mail が届かないとしておなじもにを
第三段階ときずくが増えた三角形が36個で 124/81で送り
増えた三角形が48個で 376/243 まだ送ってないので
今から送ります。
136 <私も難しかった> kasamaさん - 2003/12/01 23:02 -
あまり自信がないのですが・・・
?1辺の長さ
追加される三角形の1辺の長さは
1/3,1/9,・・・,1/n
と減少します。
?個数
直感的に(なんて言うと怒られそうですが)、
3,3*4,3*4^2,・・・,3*4^(n-1)
と増えていくと思われますの(ここがよくわかりません)。
?比の計算
??より、元の正三角形と比べて
1+3*(1/3)^2+3*4*(1/9)^2+3*4^2*(1/27)^2 = 376/243
増えています。たまたま、答えがあっただけかな?
また次のようにメールを頂きました。
<あつきパパ さん>
[answer] もとの三角形の面積をSとすると、
一次成長では、S/9の三角形が3つ増える。
また、二次成長では、S/81の三角形が12増える。
さらに、三次成長では、S/729の三角形が48増える。
よって、S+3S/9+12S/81+48S/729=376S/243
<奥入瀬 さん>
第一成長で1+1/9*3=4/3
第二成長で4/3+1/81*12=40/27
第三成長で40/27+1/729*48=376/243
法則がありそうですね。
<すてっぷ さん>
この問題に出てくる
1+(4/9)+(4/9)*(4/9)+(4/9)*(4/9)*(4/9)+・・・=?
を息子に理解してもらうために
1/2+1/4+1/8+1/16+1/32+・・・=?=1/1
1/3+1/9+1/27+1/81+・・・・・=?=1/2
1/4+1/16+1/64+・・・・・・・=?=1/3
1/5+1/25+1/125+・・・・・・・=?=1/4
・・・・・・・・・・・・・・・・・
を順番に一緒に,”算数の視点”で考えてみました。
高校で習う決まりきった方法(等比数列の和)に頼らない
で考えると,面白い景色が見えてきました。ε-δ論法です。
部分和が極限値を含む縮小区間列に含まれていました。思
わぬ収穫でした。息子にも納得してもらえたようです。そ
の後で形式的な求め方も教えました。