「今月の問題」 第56回 (平成16年5月)
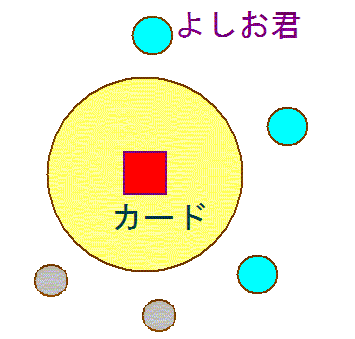
| <ルール>
①時計回りに1人ずつとる。
②上から1枚ずつ順にとる。
③テーブルには4人以上の人が座り、最高30人まで座れるとします。
|
|
上の図を見てください。円形のテーブルのまわりに、よしお君以外に何人かすわります。
そのテーブルの真ん中に、1から1000までの異なる整数が1枚ずつ書かれた1000枚のカードが、上から小さい順に重ねられている。すわった人の誰かからカードを取りはじめると、よしお君は「111」のカードも「333」のカードも「555」のカードも「777」のカードも「999」のカードも取ることができました。
ここで問題です。テーブルにすわっているのは、よしお君もふくめて何人でしょうか。
※答えが、よしお君1人だけでも問題に合うことを教えてもらい、③のルールを付け加えました。(H16.5.1 0:45)
|
<正解者一覧表>
5月31日 23:35 現在
| 正解者順位 |
name |
メール到着日時 |
備 考 |
| 1 | teki さん | 2004/5/1 0:12 | 大阪府 |
| 2 | なにわ さん | 2004/5/1 0:12 | 西宮市 |
| 3 |
ろろ さん | 2004/5/1 0:22 | 神奈川県 |
| 4 | 寺脇犬 さん | 2004/5/1 0:24 | 生駒市 |
| 5 | 経友会の進作 さん | 2004/5/1 0:33 | 京都府木津町・65歳 |
| 6 | 信三 さん | 2004/5/1 0:57 | シリコンバレーの住人 |
| 7 | ゴンとも さん | 2004/5/1 1:09 | YMOチルドレン in 豊川市 |
| 8 | oguchan1 さん | 2004/5/1 1:18 | 岡山県 |
| 9 | 奥入瀬 さん | 2004/5/1 1:55 | 東京都 |
| 10 | yan さん | 2004/5/1 9:28 | 愛知県 |
| 11 | 宮 さん | 2004/5/1 9:55 | 鹿児島県 |
| 12 | 先生の教え子 さん | 2004/5/1 13:30 | 高校2年生 |
| 13 | Michael さん | 2004/5/1 14:15 | |
| 14 | 始 受験勉強君さん | 2004/5/1 17:23 | 神奈川県 中学1年生 |
| 15 | 巷の夢 さん | 2004/5/1 17:37 | 宮城県出身 |
| 16 | teki さん | 2004/5/1 17:48 | |
| 17 | ちず さん | 2004/5/1 18:59 | 愛媛県 |
| 18 | 燕陣内 さん | 2004/5/1 20:40 | |
| 19 |
算数の森 さん | 2004/5/1 23:17 | 兵庫県 |
| 20 | 佐藤 広宣 さん | 2004/5/2 0:07 | 東京都国分寺市 |
| 21 | グランパ さん | 2004/5/2 20:24 | 木綿子のグランパ |
| 22 | まいくろん さん | 2004/5/2 20:36 | Virginiaの住人 |
| 23 | あさ ★さん | 2004/5/2 21:28 | 千葉県 |
| 24 | 吉見の沢北 さん | 2004/5/3 9:10 | 山口県出身 |
| 25 | miyoshi さん | 2004/5/3 11:35 | 愛媛県松山市 |
| 26 | ISAMU さん | 2004/5/3 16:09 | 三重県 |
| 27 | トロイ さん | 2004/5/3 21:40 | |
| 28 | スモークマン さん | 2004/5/4 0:17 | 目指せ囲碁4段! |
| 29 | 安楽 さん | 2004/5/4 3:23 | 宮崎県小林市 |
| 30 |
Hosh!kawa さん | 2004/5/5 10:23 | 滋賀生まれ大阪在住 |
| 31 | 浜田明巳 さん | 2004/5/6 8:27 | |
| 32 |
本多洋介 さん | 2004/5/6 11:36 | そろばん帝国 |
| 33 |
BossF さん | 2004/5/7 22:21 | |
| 34 | HAJI さん | 2004/5/9 1:48 | |
| 35 | ピキマキKO さん | 2004/5/9 10:07 | |
| 36 | nobu さん | 2004/5/9 22:59 | 石川県 |
| 37 | かとう さん | 2004/5/11 19:54 | 埼玉県 |
| 38 | kasama さん | 2004/5/12 14:33 | 和歌山県プログラマ |
| 39 |
あつきパパ さん | 2004/5/7 22:21 | 愛知、1歳児の父 |
| 40 | しほぉ さん | 2004/5/21 8:02 | 東京都 |
| 41 | イシタネ さん | 2004/5/21 13:27 | 60歳技術コンサルタント神奈川県小田原市 |
| 42 | 宮 さん | 2004/5/21 21:32 | |
| 43 | みかん さん | 2004/5/23 23:10 | 神奈川県 |
| 44 |
マナブ さん | 2004/5/24 11:02 | |
| 45 | すてっぷ さん | 2004/5/31 5:18 | 駑馬 |
答えは、6人でした。
<安楽さんより>
111、333、555、777、999のカードをよしお君が取るために
は
222回目に上記のカードを取らないといけないので、
222を素因数分解して2*3*37なので30人未満
という条件があるので、6人なら、37回の6倍でよしお君
に上記のカードが回ってくることが保障されます。
「30人未満」という条件を省くと、こたえが8通りでてきま
すよね。
<Hosh!kawaさんより>
n人でa番目によしお君が取るとすると、よしお君の取るカードは
n+aである。
つまり、111、333、555、777、999からaだけ引くと
nの倍数になっているはずである。
ここで、奇数から奇数を引けば偶数(2の倍数)になることと、
111、333、555、777、999が3で割れることを考えると、
これらから、3を引いても、3で割り切れ、かつ、2でも割り切れ
る。
よって、6人で3番目によしお君が取ればよい。
<浜田明巳さん>
エクセルのマクロを使って解きました.
答は6人です.人数制限を取り払うと,37,74,111,222人もありえます.でもこの人数が座るとなると,よほど大きな円卓が必要となり,現実的ではないですね.円卓の騎士じゃあるまいし.
Option Explicit
Sub Macro1()
Sheets("Sheet1").Select
Cells(1, 1).Value = 0
'
Dim ninzuu As Integer
Dim hito As Integer
Dim Yoshiokun As Integer
Dim dame As Integer
Dim card As Integer
For ninzuu = 4 To 1000 '30
dame = 0
hito = 1
card = 1
While dame = 0 And card <= 999
If card = 111 Then
Yoshiokun = hito
ElseIf (card = 333 Or card = 555 Or
card = 777 Or card = 999) And Yoshiokun <> hito Then
dame = 1
End If
card = card + 1
hito = (hito Mod ninzuu) + 1
Wend
If dame = 0 Then
Cells(1, 1).Value = Cells(1, 1).Value
+ 1
Cells(Cells(1, 1).Value, 2).Value =
ninzuu
Range("B" & Cells(1,
1).Value).Select
End If
Next ninzuu
End Sub
<BossFさんより>
取れたカードの番号の差の公約数を考えればいいから
999-777=…=333-111=222=2x6x37より 6人 答
<宮さんより>
宮と申します。毎月おもしろい問題ありがとうございます。
私の今回の解法は、333と111の差が、222ということに着目して222回目に自分の番がまわってくると考えました。
そこで、222を素因数分解した中に答えがあると考えました。
よって、222=2*3*37となる。
この中で条件が合う数は6だけである。
