乽崱寧偺栤戣乿丂戞俆俈夞丂乮暯惉侾俇擭俇寧乯
| 丂
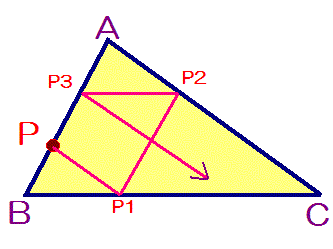
塃恾偺傛偆偵丄僌儔儞僪偵戝偒側嶰妏宍俙俛俠傪彂偒傑偟偨丅傛偟偍孨偼丄曈俙俛忋偺揰俹偐傜丄曈俙俠偵暯峴偵揰俹侾傑偱曕偒丄揰俹侾偐傜曈俙俛偵暯峴偵揰俹俀傑偱曕偒傑偡丅偙偺傛偆偵孞傝曉偟偰恑傓偲丄尦偺揰俹傑偱栠偭偰偒傑偡丅
晲孨偼丄揰俹偐傜嶰妏宍偺曈忋傪揰俛丄揰俠丄揰俙傪捠偭偰揰俹傑偱栠偭偰偒傑偡丅
晲孨偲傛偟偍孨偼丄揰俹傪摨帪偵僗僞乕僩偡傞偲丄晲孨偑揰俹偵拝偄偰偐傜丄係暘屻偵傛偟偍孨偑摓拝偟傑偡丅
偨偩偟丄傛偟偍孨偺曕偔憗偝偼枅昩侾倣丄晲孨偺恑傓懍偝傪枅昩俁倣偱偡丅
偙偙偱栤戣偱偡丅晲孨偼壗倣偺摴偺傝傪恑傫偩偺偱偟傚偆偐丅
乮仸偨偩偟丄揰P偼曈俙俛偺拞揰偱偼偁傝傑偣傫丅乯
丂
|
亙惓夝幰堦棗昞亜丂
丂丂丂丂丂丂丂丂丂丂丂
| 惓夝幰弴埵 |
丂丂丂丂値倎倣倕丂丂丂 |
丂丂儊乕儖摓拝擔帪丂丂 |
丂丂旛丂峫丂丂 |
| 丂侾 | nobu丂偝傫 | 2004/6/1丂0:08 | 愇愳導丂 |
| 丂俀 |
傠傠丂偝傫 | 2004/6/1丂0:15 | 恄撧愳導丂 |
| 丂俁 | 側偵傢丂偝傫 | 2004/6/1丂0:17 | 惣媨巗丂 |
| 丂係 | 僑儞偲傕丂偝傫 | 2004/6/1丂0:20 | YMO僠儖僪儗儞in 朙愳巗 |
| 丂俆 | teki丂偝傫 | 2004/6/1丂0:25 | 戝嶃晎丂 |
| 丂俇 | 帥榚將丂偝傫 | 2004/6/1丂1:00 | 惗嬵巗棾揷愳偺拞棳 |
| 丂俈 | 偁偝丂仛丂偝傫 | 2004/6/1丂1:15 | 愮梩導丂 |
| 丂俉 | 宱桭夛偺恑嶌丂偝傫 | 2004/6/1丂7:14 | 嫗搒晎栘捗挰丒傗偑偰俇俇嵨 |
| 丂俋 | 岼偺柌丂偝傫 | 2004/6/1丂7:33 | 媨忛導弌恎 |
| 侾侽 | 怣嶰丂偝傫 | 2004/6/1丂10:31 | 僔儕僐儞僶儗乕偺廧恖 |
| 侾侾 |
撣丂偝傫 | 2004/6/1丂11:38 | 偨偩偺悓偭傁傜偄偱庰丂 |
| 侾俀 | Michael丂偝傫 | 2004/6/1丂12:11 | 丂 |
| 侾俁 | 僗儌乕僋儅儞丂偝傫 | 2004/6/1丂17:56 | 栚巜偣埻岄係抜! |
| 侾係 | oguchan1丂偝傫 | 2004/6/1丂18:38 | 壀嶳導 |
| 侾俆 | 偪偢丂偝傫 | 2004/6/1丂18:58 | 垽昋導 |
| 侾俇 |
俿俷俵俷俙俲俬丂偝傫 | 2004/6/1丂19:06 | 戝暘導丂 |
| 侾俈 | yan丂偝傫 | 2004/6/1丂22:56 | 垽抦導丂 |
| 侾俉 | kasama丂偝傫 | 2004/6/2丂13:15 | 榓壧嶳導僾儘僌儔儅丂 |
| 侾俋 | ISAMU丂偝傫 | 2004/6/2丂17:49 | 嶰廳導丂 |
| 俀侽 | 巒 庴尡曌嫮孨丂偝傫 | 2004/6/2丂19:19 | 拞妛1擭惗
恄撧愳導丂 |
| 俀侾 | 傑偄偔傠傫丂偝傫 | 2004/6/4丂12:14 | Virginia偺廧恖丂 |
| 俀俀 | 埨妝丂偝傫 | 2004/6/4丂16:04 | 媨嶈導彫椦巗丂 |
| 俀俁 | N.Nishi丂偝傫 | 2004/6/5丂2:00 | 戝嶃晎丗拞妛嫵桜丂 |
| 俀係 | 昹揷柧枻丂偝傫 | 2004/6/5丂8:19 | 丂 |
| 俀俆 | 媨丂偝傫 | 2004/6/5丂21:24 | 幁帣搰導丂 |
| 俀俇 | 儖乕僩55丂偝傫 | 2004/6/6丂17:13 | 帬夑導丂 |
| 俀俈 | 僩儘僀丂偝傫 | 2004/6/6丂22:42 | 暫屔導丂 |
| 俀俉 | 俛妛惗丂偝傫 | 2004/6/8丂2:43 | 嶉嬍導丂棟妛晹暔棟壢妛惗丂 |
| 俀俋 | hamu丂偝傫 | 2004/6/11丂15:49 | 丂 |
| 俁侽 |
Xform丂偝傫 | 2004/6/12丂21:59 | 愮梩導戝妛侾擭惗 |
| 俁侾 | 偁傒乣偛丂偝傫 | 2004/6/13丂23:00 | 丂 |
| 俁俀 | 擕側偟丂偝傫 | 2004/6/14丂7:01 | 丂 |
| 俁俁 | 愇偩丂偝傫 | 2004/6/14丂11:58 | 嶉嬍導弔擔晹巗拞妛俁擭惗丂 |
| 俁係 | 傕偲丂偝傫 | 2004/6/14丂18:14 | 媨忛導丂 |
| 俁俆 | HAJI丂偝傫 | 2004/6/14丂21:43 | 丂 |
| 俁俇 | 偙偩偨傫丂偝傫 | 2004/6/16丂22:07 | 媨忛導嵼廧丂 |
| 俁俈 | 墱擖悾丂偝傫 | 2004/6/20丂1:34 | 搶嫗搒丂 |
| 俁俉 | kota丂偝傫 | 2004/6/24丂23:17 | 嫗搒晎丂 |
| 俁俋 | enpitukezuri丂偝傫 | 2004/6/26丂15:44 | 孮攏導丂 |
| 係侽 | 僼僕俀俈帪娫丂偝傫 | 2004/6/27丂3:23 | 崄愳導丂 |
| 係侾 | 偡偰偭傉丂偝傫 | 2004/6/30丂6:54 | 堜偺拞丂 |
摎偊偼丄俁俇侽們倣偱偟偨丅
傢偨偟偼丄偙偺栤戣偺傛偆偵暯峴偵恑傫偩傜尦偺埵抲偵栠傝丄偦偟偰偦偺挿偝偺榓偑嶰妏宍偺廃傝偺挿偝偲堦抳偡傞偙偲偵嫽枴傪帩偪傑偟偨丅埲壓偺傛偆側夝偒曽傪儊乕儖偱捀偒傑偟偨丅
亙僑儞偲傕偝傫傛傝亜
摴偺傝偼摨偠傛傝
晲巙孨偺摦偄偨帪娫傪x昩偲偡傞偲
3倶=x+240 亪 x=120昩
偙偙偱戣堄傛傝摎偊偼晲巙孨偺恑傫偩嫍棧傛傝
3*120=360m丒丒丒丒丒丒(摎偊)
亙teki偝傫傛傝亜
晲孨偲傛偟偍孨偺曕偄偨摴偺傝偑摨偠乮偙傟偼嶰妏宍偺憡帡傪棙梡
偡傟偽徹柧偱偒傑偡丅乯
亙昹揷柧枻偝傫傛傝亜
揰俹偑俹侾乮俛俠忋偺揰乯丆俹俀乮俙俠忋偺揰乯丆俹俁乮俙俛忋偺揰乯丆俹係乮俛俠忋偺揰乯丆俹俆乮俙俠忋偺揰乯丆俹'乮俙俛忋偺揰乯偲堏摦偡傞偲偡傞丏
丂暯峴慄偺惈幙偐傜丆
丂丂俙俹丗俹俛
丂亖俠俹侾丗俹侾俛
丂亖俠俹俀丗俹俀俙
丂亖俛俹俁丗俹俁俙
丂亖俛俹係丗俹係俠
丂亖俙俹俆丗俹俆俠
丂亖俙俹'丗俹'俛
丂屘偵俹偲俹'偼堦抳偡傞丏
丂丂亪俹俹侾亄俹侾俹俀亄俹俀俹俁亄俹俁俹係亄俹係俹俆亄俹俆俹
丂亖俙俹俀亄俙俹亄俛俹侾亄俹俀俠亄俹俛亄俹侾俠
丂亖(俙俹亄俹俛)亄(俛俹侾亄俹侾俠)亄(俙俹俀亄俹俀俠)
丂亖俙俛亄俛俠亄俠俙
丂屘偵晲孨偲傛偟偍孨偼嫟偵仮俙俛俠偺廃偺挿偝暘傪曕偔偙偲偵側傞丏
丂傛偟偍孨偺偐偐偭偨帪娫傪倲昩偲偡傞偲丆曕偄偨嫍棧偼丆
丂丂侾亊倲亖俁亊(倲亅係亊俇侽)
丂丂亪(俁亅侾)亊倲亖俁亊係亊俇侽
丂丂亪倲亖俁亊係亊俇侽亐(俁亅侾)亖俁俇侽乮昩乯
丂屘偵曕偄偨嫍棧偼丆
丂丂侾亊俁俇侽亖俁俇侽乮倣乯
丂俀恖偺曕偄偨嫍棧偼偦傟偧傟俁俇侽倣偱偁傞丏
乮嶲峫乯偪側傒偵揰俹偑俙俛偺拞揰偺偲偒丆拞揰楢寢掕棟偐傜丆俹俁偲俹偑堦抳偟丆傛偟偍孨偼廃偺敿暘偟偐堏摦偟側偄撪偵俹偵栠傞偙偲偵側傞丏俹偑偦傟埲奜偺偲偒偼丆偨偲偊抂揰偺俙丆俛偵堦抳偟偨偲偒偱偝偊丆忋婰偺捠傝偵側傞
丂
亙媨偝傫傛傝亜
拪徾栤戣側偺偱揔摉偵峫偊傞丅惓嶰妏宍偩偲峫偊丄嶰摍暘偟偨偲偒偺椉
幰偺嫍棧傪峫偊傞丅偦偆偡傞偲椉幰偺嫍棧偼摨偠偵側傞丅傛偭偰丄懍偝
偺斾偺媡斾偑帪娫偺斾側偺偱丄
嘊-嘆=係
嘇=係
嘆=俀
偲側傝
晲孨偺偐偐偭偨帪娫偼俀*侾=俀(暘)
傛偭偰丄嫍棧偼俀*俁*俇侽=俁俇侽(m乯
亙儖乕僩55偝傫傛傝亜
傛偟偍孨偑P3偐傜曕偄偰BC偲愙偡傞揰傪P4偲偡傞丅
仩A P P1 P2偲仩P2 P3 P4 C偼暯峴巐曈宍側偺偱曈PP1=曈AP2偐偮
曈P3P4=曈P2C
亪丂PP1+ P3P4亖AP2+ P2C丂
丂丂丂丂丂丂丂=AC
摨條偵峫偊傞偲傛偟偍孨偺曕偔嫍棧偼嶰妏宍ABC偺奜廃偲摍偟偔側
傞丅
晲孨傕戣堄傛傝嶰妏宍ABC偺奜廃傪曕偔偺偱椉幰偺曕偔嫍棧偼摍偟
偄丅
晲孨偺曕偔帪娫傪x 偲偡傞偲
傛偟偍孨偺曕偔嫍棧丂1亊60亊(x+4)
晲孨偺曕偔嫍棧丂丂丂3亊60亊x
丂丂丂丂丂丂1亊60亊(x+4)= 3亊60亊x
丂丂偙傟傪夝偄偰丂x=2
媮傔傞嫍棧偼丂3亊60亊2亖360 m
丂丂丂丂摎偊丂360 儊乕僩儖
亙俛妛惗偝傫傛傝亜
俙俛偺娫偵揰倀丆揰俹
俛俠偺娫偵揰俻丆揰俼
俠俙偺娫偵揰俽丆揰俿
傪偦傟偧傟偲傞丅
傛偟偍孨偼丂俹仺俻仺俿仺倀仺俼仺俽仺俹偺弴偵揰傪捠夁偡傞丅
俙俹亖乮俀乛俁乯俙俛偲偡傞偲丄俹俛亖乮侾乛俁乯俙俛-----------乮侾乯
仮俹俛俻佷仮俙俛俠丂乮俹俻丒俙俠偺暯峴妏偺忦審傛傝丄嶰妏崌摨乯
俹俻亖乮侾乛俁乯俙俠
仮俠俿俻佷仮俠俙俛丂乮俿俻丒俙俛偺暯峴妏偺忦審傛傝丄嶰妏崌摨乯
乮侾乯媦傃憡帡側嶰妏宍偵偍偗傞暯峴慄偺忦審傛傝丄俛俻亖乮侾乛俁乯俛俠丂俻俠亖乮俀乛俁乯俛俠
傛偭偰丄俻俿亖乮俀乛俁乯俛俙
埲壓摨條偵丄
俿倀亖乮侾乛俁乯俠俛
倀俼亖乮俀乛俁乯俙俠
俼俽亖乮侾乛俁乯俛俙
俽俹亖乮俀乛俁乯俠俛
偙偙偱丄揰俙俛俠傪娷傑側偄慄偺挿偝傪俙俛丆俛俠丆俠俙偵抲偒
姺偊傞偲丄
俹俻亄倀俼亖俠俙
俻俿亄俼俽亖俙俛
俿倀亄俽俹亖俛俠
偮傑傝丄傛偟偍孨偲晲孨偺曕偔嫍棧倃偼摍偟偄丅
偙偙偱丄傛偟偍孨偺曕偔懍偝傪倁丂晲孨偺曕偔懍偝傪倴丂乮偦傟
偧傟偺扨埵偼丂倣乛倱乯
傛偟偍孨偑曕偔帪娫傪倲亄俀係侽丂晲孨偑曕偔帪娫傪倲丂乮倲偺
扨埵偼丂昩乯
偲偡傞偲丄師偺楢棫曽掱幃偑惉傝棫偮丅
倁乮倲亄俀係侽乯亖倃
倴倲亖倃
偙偺楢棫曽掱幃傪倲偵偮偄偰夝偔偲丄
倲亖俀係侽倁乛乮倴亅倁乯
倁丒倴偵偦傟偧傟偺抣傪戙擖偡傞偲丄
倲亖侾俀侽丂乮昩乯偲側傞丅
晲孨偺曕偔懍偝偼丂俁乮倣乛倱乯丂偩偐傜丄
俁亊侾俀侽亖俁俇侽丂乮倣乯丂偑媮傔傞夝丅
亙Xform偝傫傛傝亜
晲孨偲傛偟偍孨偑曕偔嫍棧偼摍偟偄丅
偩偐傜係暘娫偱俀恖偺娫偵偱偒偨嵎偑
傛偟偍孨偑係暘娫偵曕偗傞嫍棧俀係侽倣偱偁傝丄
傑偨偦偺嵎偑偱偒傞偺偵偐偐偭偨帪娫偑侾俀侽昩偩偐傜丄
偦偺嫍棧傪傛偟偍孨偑恑傔傞嫍棧偼侾俀侽倣丅
傛偭偰晲孨偑恑傔傞嫍棧偼侾俀侽亄俀係侽亖俁俇侽倣偱偡丅
亙愇偩偝傫丄NOBU偝傫傛傝亜
摴偺傝偑摨偠側偺偱
丂
丂倶亄俀係侽亖俁倶
丂丂丂亅俀倶亖亅俀係侽
丂丂丂丂丂倶亖侾俀侽
丂丂侾俀侽亊俁亖俁俇侽丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂俁俇侽倣
丂
亙偙偩偨傫偝傫傛傝亜
栤戣傪尒偰侾乯偺傛偆偵悇嶡偟偰偐傜俀乯偺傛偆偵夝摎偟傑偟偨
1) PB=h偲偡傞乮倛亗1/2AB)
PP1+P1P2+P2P3+丒丒丒丒+PnP亖D乮倣乯偲偡傞
偙偙偱倛傪尷傝側偔0偵嬤偯偗傞偲偒丂D=BA+AC+CB偲側傝
晲孨丄傛偟偍孨嫟偵摨偠嫍棧傪堏摦偟偨偲峫偊傜傟傞
強梫帪娫偼晲孨丂D/3乮昩乯丂傛偟偍孨丂D乮昩乯
傑偨丄晲孨偺帪娫偵4暘傪壛偊偨帪娫偲傛偟偍孨偺帪娫偑摍偟偄偺偱
D/3+240亖D
亪D=360
俀乯幚嵺偵恾傪彂偄偰挷傋傞偲P6=P偲側傞偙偲偑傢偐傞
PP1丂P1P2丂P2P3丂P3P4丂P4P5丂P5P偼AB丂BC丂CA偲暯峴偵側傝
暋悢偺暯峴巐曈宍偑姰惉偡傞丄暯峴巐曈宍偺懳曈偼偦傟偧傟摍偟偄偺偱
PP1+P1P2+P2P3+P3P4+P4P5+P5P亖AB+BC+CA偲側傞丅
AB+BC+CA=D偲偡傞偲丒丒丒丒乮埲壓侾乯偲嫟捠乯
亙墱擖悾偝傫傛傝亜
憡帡傪棙梡偡傞偲丆擇恖偺恑傫偩嫍棧偼摍偟偄丅
偁偲偼柺愊恾傪彂偄偰夝偒傑偟偨丅
