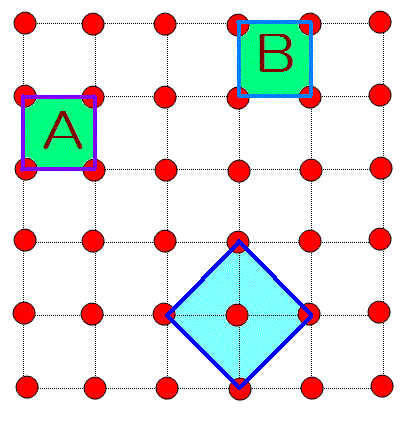
塃恾傪尒偰偔偩偝偄丅廲丄墶俆cm偺惓曽宍偵丄偦傟偧傟侾cm偢偮嬫愗偭偨奿巕偑偁傝傑偡丅
偙傟傜偺俁俇偺奿巕揰偺拞偐傜係偮慖傫偱惓曽宍傪嶌傞偙偲偵偟傑偟偨丅
偙偙偱栤戣偱偡丅壗屄偺惓曽宍傪偑弌棃傞偐峫偊偰壓偝偄丅
乮偨偩偟丄俙偲俛偼丄1cm俀偺惓曽宍偱偁傞偑俀屄偲悢偊偰偔偩偝偄丅乯
丂

| 丂
塃恾傪尒偰偔偩偝偄丅廲丄墶俆cm偺惓曽宍偵丄偦傟偧傟侾cm偢偮嬫愗偭偨奿巕偑偁傝傑偡丅 偙偙偱栤戣偱偡丅壗屄偺惓曽宍傪偑弌棃傞偐峫偊偰壓偝偄丅 乮偨偩偟丄俙偲俛偼丄1cm俀偺惓曽宍偱偁傞偑俀屄偲悢偊偰偔偩偝偄丅乯 丂 |
亙惓夝幰堦棗昞亜丂 丂丂丂丂丂丂丂丂丂丂丂
| 惓夝幰弴埵 | 丂丂丂丂値倎倣倕丂丂丂 | 丂丂儊乕儖摓拝擔帪丂丂 | 丂丂旛丂峫丂丂 |
| 丂侾 | Michael丂偝傫 | 2004/7/1丂0:24 | 丂 |
| 丂俀 | 撣偪傖傫偼僇僢僷側偺偝傫 | 2004/7/1丂0:36 | 僇僢僷偱庰丂 |
| 丂俁 | 僼僕俀俈帪娫丂偝傫 | 2004/7/1丂0:40 | 崄愳導丂 |
| 丂係 | 僑儞偲傕丂偝傫 | 2004/7/1丂0:51 | YMO僠儖僪儗儞 in 朙愳巗 |
| 丂俆 | teki丂偝傫 | 2004/7/1丂8:25 | 戝嶃晎丂 |
| 丂俇 | 墱擖悾丂偝傫 | 2004/7/1丂1:38 | 搶嫗搒丂 |
| 丂俈 | 傠傠丂偝傫 | 2004/7/1丂9:04 | 恄撧愳導丂 |
| 丂俉 | 宱桭夛偺恑嶌丂偝傫 | 2004/7/1丂11:24 | 嫗搒晎栘捗挰丒俇俇嵨丂 |
| 丂俋 | 儌儖儌僢僩憹怋拞丂偝傫 | 2004/7/1丂11:50 | 儌儖儌僢僩嫟榓崙丂 |
| 侾侽 | ISAMU丂偝傫 | 2004/7/1丂12:00 | 嶰廳導丂 |
| 侾侾 | 岼偺柌丂偝傫 | 2004/7/1丂12:02 | 丂 |
| 侾俀 | 偁偝丂仛丂偝傫 | 2004/7/1丂15:32 | 愮梩導丂 |
| 侾俁 | 傒偐傫丂偝傫 | 2004/7/1丂18:20 | 丂 |
| 侾係 | 巒 庴尡曌嫮孨丂偝傫 | 2004/7/1丂18:54 | 恄撧愳導丂 |
| 侾俆 | N.Nishi丂偝傫 | 2004/7/1丂23:39 | 戝嶃晎丗拞妛嫵桜丂 |
| 侾俇 | kasama丂偝傫 | 2004/7/2丂14:58 | 榓壧嶳導僾儘僌儔儅丂 |
| 侾俈 | 偪偢丂偝傫 | 2004/7/3丂15:45 | 垽昋導丂 |
| 侾俉 | nobu丂偝傫 | 2004/7/3丂20:47 | 丂 |
| 侾俋 | 俛妛惗丂偝傫 | 2004/7/4丂1:05 | 暔棟壢偺偔偣偵旝暘曽掱幃偺夝偗側偄僟儊妛惗 |
| 俀侽 | Xform丂偝傫 | 2004/7/4丂23:16 | 岺妛宯戝妛1擭惗丂僥僯僗惙傝偐傕 |
| 俀1 | 嶼悢偺怷丂偝傫 | 2004/7/7丂15:52 | 暫屔導 |
| 俀俀 | 怣嶰丂偝傫 | 2004/7/11丂18:01 | 僔儕僐儞僶儗乕偺廧恖 |
| 俀俁 | 昹揷柧枻丂偝傫 | 2004/7/15丂14:11 | 丂 |
| 俀係 | 埨妝丂偝傫 | 2004/7/22丂15:48 | 丂 |
| 俀俆 | 偁傒乣偛丂偝傫 | 2004/7/24丂23:46 | 摽搰導丂 |
| 俀俇 | Ishihara丂偝傫 | 2004/7/26丂13:36 | 丂 |
摎偊偼丄侾侽俆庬椶偱偟偨丅
亙撣偪傖傫偼僇僢僷側偺偝傫傛傝亜
俀俆亄侾俇亊俀亄俋亊俁亄係亊係亄侾亊俆
丂
亙僑儞偲傕乮YMO僠儖僪儗儞 in 朙愳巗乯偝傫傛傝亜
愭偢丄幬傔偱側偄傕偺偼
1曈偑1cm偺惓曽宍偼25屄
2cm偼16屄,3cm偼9屄,4cm偼4屄,5cm偼1屄
埲忋傛傝
25+16+9+4+1=55屄丒丒丒丒丒丒嘆
師偵幬傔偺傕偺偼
1,1偺惓曽宍偺懳妏慄傪1曈偵傕偮傕偺偼16屄
2,2偺惓曽宍偺懳妏慄傪1曈偵傕偮傕偺偼4屄
1,2偺挿曽宍偺懳妏慄傪1曈偵傕偮傕偺偼9*2=18屄
1,3偺挿曽宍偺懳妏慄傪1曈偵傕偮傕偺偼4*2=8屄
1,4偺挿曽宍偺懳妏慄傪1曈偵傕偮傕偺偼1+1=2屄
2,3偺挿曽宍偺懳妏慄傪1曈偵傕偮傕偺偼1+1=2屄
埲忋傛傝
16+4+18+8+2+2=50屄
偙傟偲嘆偲傛傝50+55=105屄
丂
亙teki丂偝傫傛傝亜
堦斒揑偵値亊値偺奿巕揰傪寢傫偱偱偒傞惓曽宍偺屄悢N偼丄埲壓偺
幃偱昞偣傑偡丅
N亖値丱2*乮値丱2丂-1乯/12
値亖俇傪戙擖偡傞偲丄N=105
亙傠傠丂偝傫傛傝亜
孹偒偺側偄惓曽宍偐傜彫偝偄弴偵
俆倶俆亄係倶係亄俁倶俁亄俀倶俀亄侾亖俆俆
捀揰傪堦屄偢偮偢傜偟偨僟僀儎宆偑彫偝偄弴偵
係倶係亄俀倶俀亖俀侽
捀揰傪堦曽偑俀屄堦曽偑侾屄偢傜偟偨傕偺偑
俁倶俁倶俀亖侾俉
捀揰傪堦曽偑俁屄堦曽偑侾屄偢傜偟偨傕偺偑
俀倶俀倶俀亖俉
捀揰傪堦曽偑係屄堦曽偑侾屄偢傜偟偨傕偺偑
侾倶俀亖俀
捀揰傪堦曽偑俀屄堦曽偑俁屄偢傜偟偨傕偺偑
侾倶俀亖俀
偁傢偣偰
俆俆亄俀侽亄侾俉亄俉亄俀亄俀亖侾侽俆
丂
亙宱桭夛偺恑嶌丂偝傫傛傝亜
乮侾乯堦曈偑惍悢偺応崌偺屄悢
丂丂丂偙傟偼幬妏搙娭學側偟
丂丂丂侾們倣*侾們倣偺傕偺丒丒丒俀俆
丂丂丂俀們倣*俀們倣偺傕偺丒丒丒侾俇
丂丂丂俁們倣*俁們倣偺傕偺丒丒丒丂俋
丂丂丂係們倣*係們倣偺傕偺丒丒丒丂係
丂丂丂俆們倣*俆們倣偺傕偺丒丒丒丂侾
乮俀乯堦曈偑併俀偺惍悢攞偺応崌偺屄悢
丂丂丂偙傟偼幬妏搙娭學側偟
丂丂丂併俀們倣*併俀們倣偺傕偺丒丒丒丒丒丒侾俇
丂丂丂俀併俀們倣*俀併俀們倣偺傕偺丒丒丒丂係
乮俁乯堦曈偑併俀偺惍悢攞偱側偄応崌偺屄悢
丂丂丂偙傟偼幬妏搙娭學偁傝丅
丂丂丂幬妏搙偑媡偺傕偺偑偁傞偺偱俀攞偡傞丅
丂丂丂併俆們倣*併俆們倣偺傕偺丒丒丒丒丒丒侾俉
丂丂丂併侾侽們倣*併侾侽們倣偺傕偺丒丒丒丂俉
丂丂丂併侾俁們倣*併侾俁們倣偺傕偺丒丒丒丂俀
丂丂丂併侾俈們倣*併侾俈們倣偺傕偺丒丒丒丂俀
丂丂丂埲忋崌寁侾侽俆屄偱偡丅
亙俛妛惗丂偝傫傛傝亜
36屄偺奿巕傪6師偺惓曽峴楍
a11 a12 a13 a14 a15 a16
a21 丂丂丂乧丂丂丂丂a26
乧丂丂丂丂乧丂丂丂丂乧
a61丂丂丂 乧丂丂丂丂a66
偲尒棫偰丄i峴j楍偺惉暘傪俙ij偲彂偔偲偡傞丅
(1)
4偮偺妏傪丄廲偼摨偠j楍丄墶偼摨偠i峴偺惉暘摨巑偱宷偓丄4曈偼
慡偰摍偟偄挿偝偺巐妏宍偵偮偄偰峫偊傞丅
偙傟偼丄1曈偺挿偝偑ncm乮偨偩偟丄n偼1偐傜5傑偱偺惍悢乯偺惓曽
宍偱偁傞丅
曈偺挿偝偵傛偭偰5庬椶偺惓曽宍偵暘偗傞偲丄
36屄偺奿巕撪偵懚嵼偱偒傞惓曽宍偺戝偒偝偲偦偺悢偼
5cm 仺 1
4cm 仺 4
3cm 仺 9
2cm 仺 16
1cm 仺 25
懚嵼偡傞偺偱丄1曈偺挿偝偑ncm偺惓曽宍偼55屄
(2)
俙ij傪拞怱偲偟丄偦偙偐傜忋壓嵍塃偵摍偟偔m偩偗棧傟偨埵抲偵峴
楍惉暘偑懚嵼偡傞巐妏宍偵偮偄偰峫偊傞丅乮m偼帺慠悢乯
俙i-m j丂俙i j+m丂俙i j-m丂俙i+m j丂傪妏偲偡傞巐妏宍偲側
傝丄偙傟偵懳妏慄傪堷偒丄4偮偺嶰妏宍傪嶌傞丅
偙偺4偮偺嶰妏宍偼慡偰捈妏擇摍曈嶰妏宍偱偁傞偐傜丄傕偲偺巐妏
宍偼1曈傪嶰妏宍偺幬曈偺挿偝m併2cm偲偡傞惓曽宍丅
懳妏慄偺挿偝2m偵偮偄偰丄1亝2m亝5丂偐偮丂m偼帺慠悢偱偁傞偐
傜丄 m=1,2
傛偭偰丄傕偲偺惓曽宍偺1曈偺挿偝偼 併2,2併2丂偺2庬椶丅
俙ij傪拞怱偲偟丄俙i亇1 j亇1丂傑偨偼丂俙i亇2 j亇2丂偵惉暘偑
懚嵼偡傞傕偺傪庢傝弌偡偲丄
俙22乣俙25丂俙32 俙35 俙42 俙45 俙52乣俙53 偵偼忋壓嵍塃
摍偟偄嫍棧偵1偮偯偮惉暘偑懚嵼丄
俙33 俙34 俙43 俙44丂偼忋壓嵍塃摍偟偄嫍棧偵2偮偯偮惉暘偑
懚嵼偡傞
偮傑傝丄寁20屄偑1曈偺挿偝傪 m併2 cm 偲偡傞惓曽宍偺悢偲側
傞丅
(3)
偦偺懠偺惓曽宍
(1)偺巐妏宍偺偆偪丄嵟傕嵍忋偵埵抲偡傞妏傪俙ij偲偡傞丅
1亝n亝3丂2亝i亝4丂2亝j亝4丂3亝i+n亝5丂3亝j+n亝5偲偟丄
俙i-1 j丂俙i j+n+1丂俙i+n+1 j+n丂俙i+n j-1 丂乮i,j,n偼慡偰
帺慠悢乯---------嘆
傪慄暘偱宷偖偲丄偙偺4揰傪妏偲偡傞惓曽宍偲側傞丅
亂徹柧亃
巐妏宍俙i-1 j丂俙i j+n+1丂俙i+n+1 j+n丂俙i+n j-1丂偵偍偄
偰丄
惓曽宍俙ij丂俙i j+n丂俙i+n j+n丂俙i+n j丂傪偲傝丄
嶰妏宍俙i-1 j丂俙ij丂俙i j+n+1
嶰妏宍俙i j+n+1丂俙i j+n丂俙i+n+1 j+n
嶰妏宍俙i+j+1 j+n丂俙i+n j+n丂俙i+n j-1
嶰妏宍俙i+n j-1丂俙i+n j丂俙i-1 j
傪嶌傞丅
4偮偺嶰妏宍偼曈偺挿偝偑1cm n+1cm偺捈妏嶰妏宍側偺偱丄擇曈嫴
妏傛傝崌摨丅
傑偨丄4偮偺嶰妏宍偵偮偄偰丄捈妏埲奜偺2妏傪P丒Q偲偡傞偲丄
180-(P+Q)=90
偱偁傞偐傜丄傕偲偺巐妏宍偼4妏慡偰偑捈妏丄崌摨側嶰妏宍偺幬曈
偑4曈偲側傞丄
1曈偺挿偝偑併{1^2+(n+1)^2}cm偺惓曽宍丅嘆偺忦審傪傒偨偡嶰妏宍偼15屄丅
傑偨丄俙i j-1丂俙i+1 j+n丂俙i+n j+n+1丂俙i+n-1 j
偵偮偄偰傕摨條偵偡傞偲丄15屄偺惓曽宍偑偲傟傞丅
傛偭偰丄庢傝偆傞慡偰偺惓曽宍偺悢偼50+25+15+15=105屄
亙kasama丂偝傫傛傝亜
僾儘僌儔儉偱挷傋傑偟偨丅堦曈偺挿偝:屄悢偼丄埲壓偺捠傝偱偟偨丅
1cm:25屄丄併2cm:16屄丄2cm:16屄丄併5cm:18屄丄2併2cm:4屄丄
3cm:9屄丄併10cm:8屄丄併13cm:2屄丄4cm:4屄丄併17cm:2屄丄5cm:1屄
埲忋丄105屄偱偡偹
亙Xform丂偝傫傛傝亜
1儅僗暘丄2儅僗暘丒丒丒5儅僗暘偺挿偝傪侾曈偲偡傞惓曽宍偑
25+16+9+4+1=55
偦偟偰侾儅僗偺懳妏慄偱偱偒傞惓曽宍丄俀亊俀儅僗偺惓曽宍偺懳
妏慄偱偱偒傞惓曽宍偑16+4=20
師偵俀儅僗偺挿曽宍偺懳妏慄傪侾曈偲偡傞惓曽宍偑偁傝丄摨條偵
俁儅僗偺挿曽宍丄係儅僗偺挿曽宍偲峫偊傞偲9+4+1=14
偨偩偟丄懳妏慄偺庢傝曽偼俀捠傝偩偐傜偦偺俀攞偺俀俉屄丅
俀亊俁儅僗偺挿曽宍偺懳妏慄偱偱偒傞惓曽宍傪峫偊傞偲俀屄丅
偙傟傜偑偱偒傞惓曽宍偺偡傋偰側偺偱丄慡晹懌偡偲
55+20+28+2=105屄偲側傝傑偡丅
亙嶼悢偺怷丂偝傫傛傝亜
宯摑棫偰偰悢偊忋偘傑偟偨丅
場傒偵丄杮栤傪堦斒壔偟偨乮俁俇屄傪俶亊俶屄偵偟偨乯栤戣偺摎
偊偼侾/侾俀亊俶亊俶亊乮俶亅侾乯亊乮俶亄侾乯偲側傝傑偡偹丅
亙昹揷丂柧枻偝傫傛傝亜
丂僄僋僙儖偺儅僋儘偱夝偒傑偟偨丏
Option Explicit
Sub Macro1()
Sheets("Sheet1").Select
Cells(1, 1).Value = 0
Range("A1").Select
'
Dim hen As Integer
Dim j1 As Integer
Dim j2 As Integer
Dim j3 As Integer
For j1 = 1 To 6 - 1
For j2 = j1 + 1 To 6
hen = j2 - j1
For j3 = 1 To 6 - hen
Cells(1, 1).Value = Cells(1, 1).Value + 1
Cells(Cells(1, 1).Value, 2).Value = chouten(j3, j1)
Cells(Cells(1, 1).Value, 3).Value = chouten(j3, j2)
Cells(Cells(1, 1).Value, 4).Value = chouten(j3 + hen, j2)
Cells(Cells(1, 1).Value, 5).Value = chouten(j3 + hen, j1)
Next j3
Next j2
Next j1
'
For j1 = 2 To 6 - 1
For j2 = 1 To Application.Min(j1 - 1, 6 - j1)
For j3 = 1 To 6 - j2 * 2
Cells(1, 1).Value = Cells(1, 1).Value + 1
Cells(Cells(1, 1).Value, 2).Value = chouten(j3, j1)
Cells(Cells(1, 1).Value, 3).Value = chouten(j3 + j2, j1 + j2)
Cells(Cells(1, 1).Value, 4).Value = chouten(j3 + j2 * 2, j1)
Cells(Cells(1, 1).Value, 5).Value = chouten(j3 + j2, j1 - j2)
Next j3
Next j2
Next j1
End Sub
Private Function strr(ByVal n As Integer) As String
strr = Right(Str(n), Len(Str(n)) - 1)
End Function
Private Function chouten(ByVal x, ByVal y As Integer) As String
chouten = "(" + strr(x) + "," + strr(y) + ")"
End Function