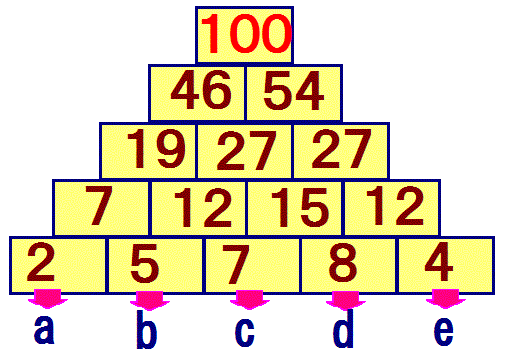
左図を見てください。5段の積み木がピラミッド状に積んであります。一番下の段には、1桁の異なった1~9の数字が書いてあります。
上に積まれた数字は、下段の2つの積み木の数字の和を記入していきます。
このようにして計算していくと、一番上の数字は100になります。このように下段のa~eに異なった数字を入れて100になる組み合わせは172種類(?)になるようです。
ここで問題です。(a+b+c+d+e)が最小になるときいくらになるでしょうか。

| 左図を見てください。5段の積み木がピラミッド状に積んであります。一番下の段には、1桁の異なった1~9の数字が書いてあります。 ここで問題です。(a+b+c+d+e)が最小になるときいくらになるでしょうか。 |
<正解者一覧表>
| 正解者順位 | name | メール到着日時 | 備 考 |
| 1 | nobu さん | 2004/8/1 0:07 | |
| 2 | 寺脇犬 さん | 2004/8/1 0:07 | 生駒市 |
| 3 | みかん さん | 2004/8/1 0:11 | 神奈川県 |
| 4 | ろろ さん | 2004/8/1 0:14 | 神奈川県 |
| 5 | フジ27時間 さん | 2004/8/1 0:22 | 香川県 |
| 6 | 奥入瀬 さん | 2004/8/1 0:38 | 東京都 |
| 7 | 信三 さん | 2004/8/1 3:01 | シリコンバレーの住人 |
| 8 | ゴンとも さん | 2004/8/1 4:02 | YMOチルドレンin豊川市 |
| 9 | 呑 さん | 2004/8/1 4:32 | 前世はカッパのナメクジ男 |
| 10 | N.Nishi さん | 2004/8/1 7:14 | 大阪府:中学教諭 |
| 11 | Michael さん | 2004/8/1 9:39 | |
| 12 | 経友会の進作 | 2004/8/1 10:15 | 京都府木津町・66歳 |
| 13 | なにわ さん | 2004/8/1 12:15 | 西宮市 |
| 14 | 巷の夢 さん | 2004/8/1 14:29 | 宮城県出身 |
| 15 | ちず さん | 2004/8/1 15:11 | 愛媛県 |
| 16 | teki さん | 2004/8/1 15:55 | 大阪府 |
| 17 | あみ~ご さん | 2004/8/2 0:38 | |
| 18 | ブギ さん | 2004/8/2 9:20 | |
| 19 | kasama さん | 2004/8/2 13:37 | 和歌山県プログラマ |
| 20 | なか さん | 2004/8/2 16:16 | 北海道 |
| 21 | ISAMU さん | 2004/8/2 18:35 | 三重県 |
| 22 | 浜田明巳 さん | 2004/8/3 8:44 | |
| 23 | Mr.X さん | 2004/8/5 7:04 | 山梨県韮崎市 |
| 24 | テモ さん | 2004/8/7 23:04 | |
| 25 | 宮 さん | 2004/8/8 12:21 | 鹿児島県 |
| 26 | 安楽 さん | 2004/8/9 1:29 | |
| 27 | すてっぷ さん | 2004/8/9 1:42 | 井の中 |
| 28 | トロイ さん | 2004/8/10 23:09 | |
| 29 | nan-nanさん | 2004/8/12 21:19 | |
| 30 | 始 受験勉強君 さん | 2004/8/13 22:00 | 中学1年生 神奈川県 |
| 31 | oguchan1 さん | 2004/8/14 0:14 | |
| 32 | ナルとも さん | 2004/8/17 22:26 | 愛知県 |
| 33 | hima さん | 2004/8/21 18:29 | 長崎県 |
| 34 | 雀鬼 さん | 2004/8/22 4:51 | 埼玉県在住 医大生 |
| 35 | 小林 祥久 さん | 2004/8/29 18:49 | 埼玉に住んでまーす |
| 36 | ほげ さん | 2004/8/31 15:52 | 北の隠れ家 |
答えは24です。
<雀鬼 さんの回答>
一番下の段をa,b,c,d,eとおくと、題意より、a+4b+6c+4d+e=100…①である。a+b+c+d+e≦23…②と仮定すると②より3(b+d)+5c≧77…③、1≦b,c,d≦9かつa,b,c,d,eが異なる1~9の数字であることから,a+e≧3であり、b+c+d≦20であることがわかる。
したがって、3b+3c+3d≦60…④、③式と比べると、C=9でなければ③,④が成立しない,すると、③,④が成り立つためにb+c=11でなければならない。このとき①よりa+e=2、しかし、題意より、2は不適である。
ゆえにa+b+c+d+e≧24である。
また(a,b,c,d,e)=(1,5,8,7,3)のときなどa+b+c+d+e=24となり、かつ題意を満たすので、a+b+c+d+eの最小値は24である。(q.e.d)
<ナルとも さんの回答>
和の最小値を考えるので、c>b or d>a or eとして差し支えない。
cが7以下では和が100に満たない為、cは8か9となる。この中で最小値を考え
ると
1、3、5、7、8となり最小値は24
<始 受験勉強君 さんの回答>
解法
図は上に積まれた数字は、下段の2つの積み木の数字の和を記入していっているので、
100=a+4b+6c+4d+e・・・・①
①よりcをできるだけ大きくした方がいいことが分かる。よってcは9だとして考える。
100-9×6=46
46以下の4の倍数は44。よって
b+d=11
したがって
a+e=100-54-44=2
しかしa~eの中に同じ数があってはいけないので
a+e=4(a、eのどちらかが3)
合計は102になる。
ここで、c=8だとして考える。
102-6=96
100-96=4
よって
b+d=12
c=8
a+e=4
∴a+b+c+d+e=12+8+4=24
a~eまでは20通りになりますが、僕の例では
a=1,b=5,c=8,d=7,e=3としました
<宮さんの回答>
100=a+4b+6c+4d+e
100=a+e+4(b+d)+6c
Cの係数が6でもっとも大きいので、6Cがなるべく大きな値になるよ
うな数字から代入していく。そうするとC=8のとき、最小値24とな
る。
<Mr.Xさんの回答>。
8月の問題に解答します。
(a+e)+4(b+d)+6c=100
a+b+c+d+e を最小にする
(a+e)は偶数で、a≠e a+e=4
cは4の倍数で、c=8
(b+d)=12
a+b+c+d+e の最小値は24です。
<浜田明巳さんの回答>
エクセルのマクロで解きました.答は24.a~eは次の4通りあります.
1, 5, 8, 7, 3
1, 7, 8, 5, 3
3, 5, 8, 7, 1
3, 7, 8, 5, 1
Option Explicit
Sub Macro1()
Sheets("Sheet1").Select
Cells(1, 1).Value = 0 'a~eの組数
Cells(2, 1).Value = 0 '答の個数
Range("A2").Select
Dim a As Integer
Dim b As Integer
Dim c As Integer
Dim d As Integer
Dim e As Integer
Dim f As Integer
Dim g As Integer
Dim h As Integer
Dim i As Integer
Dim j As Integer
Dim k As Integer
Dim l As Integer
Dim m As Integer
Dim n As Integer
Dim o As Integer
Dim wa As Integer
Dim min As Integer
min = 1000
For a = 1 To 9
For b = 1 To 9
If a <> b Then
For c = 1 To 9
If a <>
c And b <> c Then
For d = 1 To 9
If a <> d And b <> d And c <> d Then
For e = 1 To 9
If a <> e And b <> e And c <> e And d <> e Then
f = a + b
g = b + c
h = c + d
i = d + e
j = f + g
k = g + h
l = h + i
m = j + k
n = k + l
o = m + n
If o = 100 Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
wa = a + b + c + d + e
If min > wa Then
min = wa
Columns("B:F").Select
Selection.ClearContents
Range("G1").Select
Cells(2, 1).Value = 1
Cells(1, 2).Value = a
Cells(1, 3).Value = b
Cells(1, 4).Value = c
Cells(1, 5).Value = d
Cells(1, 6).Value = e
Cells(1, 7).Value = wa
ElseIf min = wa Then
Cells(2, 1).Value = Cells(2, 1).Value + 1
Range("G" & Cells(2, 1).Value).Select
Cells(Cells(2, 1).Value, 2).Value = a
Cells(Cells(2, 1).Value, 3).Value = b
Cells(Cells(2, 1).Value, 4).Value = c
Cells(Cells(2, 1).Value, 5).Value = d
Cells(Cells(2, 1).Value, 6).Value = e
Cells(Cells(2, 1).Value, 7).Value = wa
End If
End If
End If
Next e
End If
Next d
End If
Next c
End If
Next b
Next a
End Sub
<なかさんの回答>
a+e + 4(b+d) + 6c = 100 より、
c に大き目の数を割り当てるのが効率的なのですが、
c = 9 とすると、4 で割った余りからみて a+e = 6
が必要になり、c = 8 案に負けます。
1 + 4 + 9 + 6 + 5 = 25 ×
1 + 5 + 8 + 7 + 3 = 24 ○
<経友会の進作さんの回答>
(1)ピラミッド状につまれている合計100の積み木を
a、b、c、d、e で表示すると、a+4b+6c+4d+e=100。
(2)a+b+c+d+e を最小にするためには、c、b、d が
大きな数であることが必要。
c=9の場合は、a+b+c+d+e=25が最小。
c=8の場合は、a+b+c+d+e=24が最小。
その他の場合は、a+b+c+d+e>24
以上よりa+b+c+d+e=24が最小です。
<寺脇犬さんの回答>
答えは 24ですが、 0も使っていいなら 22が最小ですね。
たとえば A2、B4、C9,D7,E0
僕は、 A+4B+6C+4D+E=100として
覆面算に見立てて解きました。
<tekiさんの回答>
100=a+4b+6c+4d+eより
cを9とした場合
最小は、a+e=6 b+d=10 c=9 で25
ところが、cを8とした場合
最小は、a+e=4 b+d=12 c=8 で24
こちらの方が小さくなりますね。
<ゴンともさんの回答>
先ず、題意の積み木の5段目を左からa,b,c,d,eと置くと
1から5段までは以下
a+4*b+6*c+4*d+e 1段目
a+3*b+3*c+d,b+e+3*c+3*d 2段目
a+c+2*b,b+d+2*c,c+e+2*d 3段目
a+b,b+c,c+d,d+e 4段目
a,b,c,d,e 5段目
ここで題意で1段目が100より
a+4*b+6*c+e+4*d=100・・・・・・①
これを満たすa,b,c,d,eは
先ず、
c=1:a+4*b+e+4*d=94 4(b+d)+a+e=94(不可) ∵ 4(b+d)+a+eの最大値はb+d=17,a+e=13で4*17+13=81
c=2:a+4*b+e+4*d=88 4(b+d)+a+e=88(不可) ∵ 4(b+d)+a+eの最大値はb+d=17,a+e=13で4*17+13=81
c=3:a+4*b+e+4*d=82 4(b+d)+a+e=82(不可) ∵ 4(b+d)+a+eの最大値はb+d=17,a+e=13で4*17+13=81
c=4:a+4*b+e+4*d=76 4(b+d)+a+e=76
b+d=17,a+e=8 a+b+c+d+e=29
b+d=16,a+e=12 a+b+c+d+e=32
b+d=15,a+e=16 a+b+c+d+e=35
あとのcの値のものはb+dが1少なくなるとa+eが4あがり+3よりb+dが題意を満たし最大のもだけ考えればよい
c=5:a+4*b+e+4*d=70 4(b+d)+a+e=70
b+d=16,a+e=6 a+b+c+d+e= 27
c=6:a+4*b+e+4*d=64 4(b+d)+a+e=64
b+d=15,a+e=4 a+b+c+d+e=25
c=7:a+4*b+e+4*d=58 4(b+d)+a+e=58
b+d=13,a+e=6 a+b+c+d+e=26
c=8:a+4*b+e+4*d=52 4(b+d)+a+e=52
b+d=12,a+e=4 a+b+c+d+e=24
c=9:a+4*b+e+4*d=46 4(b+d)+a+e=46
b+d=10,a+e=6 a+b+c+d+e=25
以上よりa+b+c+d+e=24・・・・・・(答え)(b+d=12,a+e=4,c=8)
検算(∵ちゃんと文字でおいたので検算はいらないですが途中間違えならでてこないので(1例))
100 O.K.
43+57
15+28+29
04+11+17+12
01+03+08+09+03