「今月の問題」 第61回 (平成16年10月)
| 今年は台風がたくさん上陸しました。そこで、今月は台風を題材にします。
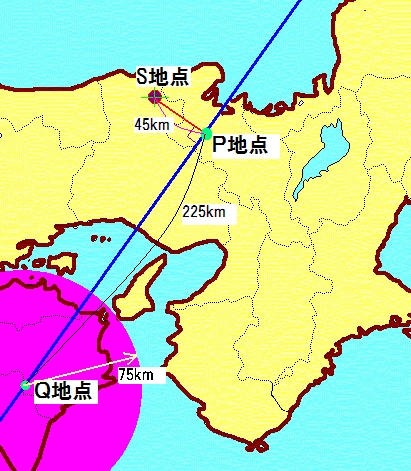
「台風は,午前0時現在,中心がP地点の南西225kmの高知と徳島の県境のQにあり,時速30kmで北東へ進んでいます。中心から半径75km以内は暴風域となっています。」
S地点に住むよしお君の家から台風の進路予想線への最短地点であるP地点までの距離は45km離れています。よしお君は,S地点が暴風域に入る時刻などを予想しました。
ここで問題です。S地点が暴風域から完全にぬけるのは午前何時何分になるでしょうか。
ただし、
・暴風域は,台風の中心から半径75kmの円の周及び内部とする。
・台風の進む向き・速さ,暴風域の大きさは変わらないものとする。
(答えは、午前6時32分でしたら、6:32 という形で答えていただければと思います。)
|
答を見つけた方は、以下のアドレスへメールを下さい。正答でしたら、ご連絡させていただきますので宜しくお願いします。
また、フォーム
を利用されても、回答を受けています。
正解者認証
<※1>ハンドルネームを書いて下さい!
<※2>順位表にホームページへのリンクを貼り付けていい方はURLをお書き添えください。
<※3>都道府県名や職業など知らせてもらえたら有り難いですが。
なお、締め切りは10月31日といたします。
次回の出題予定は、平成16年11月1日 0:00を予定しています。
 yoshioka@mxa.nkansai.ne.jp
yoshioka@mxa.nkansai.ne.jp
<正解者一覧表>
10月31日 22:57 現在
| 正解者順位 |
name |
メール到着日時 |
備 考 |
| 1 | 佐藤 広宣 さん | 2004/10/1 0:07 | |
| 2 |
ろろ さん | 2004/10/1 0:10 | 神奈川県 |
| 3 |
mhayashi さん | 2004/10/1 0:12 | 大阪府 |
| 4 | 寺脇犬 さん | 2004/10/1 0:15 | 生駒市 |
| 5 | nobu さん | 2004/10/1 0:16 | |
| 6 | でぐ さん | 2004/10/1 0:17 | |
| 7 | フジ27時間 さん | 2004/10/1 0:17 | 香川県 |
| 8 | Gakkun さん | 2004/10/1 0:25 | 広島県高校生テニス部 |
| 9 | ゴンとも さん | 2004/10/1 1:03 | |
| 10 | 奥入瀬 さん | 2004/10/1 1:08 | 東京都 |
| 11 | 経友会の進作 さん | 2004/10/1 5:48 | 京都府木津町・66歳 |
| 12 | 巷の夢 さん | 2004/10/1 7:30 | 宮城県出身 |
| 13 | ISAMU さん | 2004/10/1 9:33 | 三重県 |
| 14 | 信三 さん | 2004/10/1 10:31 | シリコンバレーの住人 |
| 15 | kasama さん | 2004/10/1 10:33 | 和歌山県プログラマ |
| 16 | スモークマン さん | 2004/10/1 13:32 | 目指せ囲碁4段 |
| 17 | 日本酒 さん | 2004/10/1 15:16 | 島根県 |
| 18 | Mr.X さん | 2004/10/1 15:52 | 山梨県韮崎市 |
| 19 | なにわ さん | 2004/10/1 17:41 | 西宮市 |
| 20 | 小林 祥久 さん | 2004/10/1 20:49 | |
| 21 | 燕陣内 さん | 2004/10/1 21:22 | 奈良県中部 |
| 22 | Michael さん | 2004/10/1 23:24 | |
| 23 | すてっぷ さん | 2004/10/2 0:00 | |
| 24 | N.Nishi さん | 2004/10/2 7:16 | 大阪府:中学教諭 |
| 25 | ぶぎぱぱ さん | 2004/10/2 10:56 | 神奈川県 |
| 26 | プロビーム さん | 2004/10/2 18:10 | 埼玉県熊谷市 |
| 27 | もぐらっこ さん | 2004/10/2 20:15 | |
| 28 | 勇水 さん | 2004/10/2 23:45 | 高知県土佐山田町 |
| 29 | oguchan1 さん | 2004/10/3 3:54 | 岡山県 |
| 30 | 宮 さん | 2004/10/3 16:32 | 鹿児島県 |
| 31 | 922 さん | 2004/10/3 22:05 | 兵庫県赤穂郡 |
| 32 | Plutonian さん | 2004/10/4 2:00 | 冥界より |
| 33 | 浜田明巳 さん | 2004/10/4 9:04 | |
| 34 |
あつきパパ さん | 2004/10/4 10:35 | 愛知県、1歳児の父 |
| 35 | MARORINE さん | 2004/10/6 13:23 | 福岡 塾講師→京都 大学生 |
| 36 |
なか さん | 2004/10/6 14:17 | 北海道 |
| 37 | 安楽 さん | 2004/10/6 15:28 | |
| 38 | ちず さん | 2004/10/6 15:39 | 愛媛県 |
| 39 |
高田一輝(姉小路) さん | 2004/10/6 14:17 | 愛知県在住、中2 |
| 40 |
ほげ さん | 2004/10/8 17:59 | 北の隠れ家 |
| 41 | マナパパ さん | 2004/10/9 10:34 | |
| 42 | JDEAN さん | 2004/10/11 14:07 | 兵庫県出身、東京在住。エンジニア |
| 43 | 123 さん | 2004/10/12 16:23 | 栃木県 |
| 44 | TOM さん | 2004/10/17 2:29 | 千葉の某塾の数学講師 |
| 45 | AMEI さん | 2004/10/19 18:53 | |
| 46 | akira さん | 2004/10/23 11:47 | |
| 47 | じょーじ さん | 2004/10/28 17:26 | 東京 |
| 48 |
おとぼけ呑ちゃん さん | 2004/10/29 11:52 | 日本酒の季節じゃ~ |
| 49 | 始 受験勉強君 さん | 2004/10/31 16:00 | 神奈川県 中学1年生 |
| 50 | ルート55 さん | 2004/10/31 22:57 | 滋賀県 |
答えは、午前9時30分でした。
<ゴンとも さんより>
先ず、題意の図でQ地点を
(0,0),P地点を(225,0)
S地点を
(225,45)・・・・・・①として
xy座標に乗せると
暴風域は
(x-30*t)^2+y^2<75^2=5625
(ここでt(時間))
①でこの不等式とより
(225-30*t)^2+45^2<5625
900*t^2-13500*t+47025<0
11/2<t<19/2
より19/2時間は9.5時間で9時30分
<経友会の進作 さんより>
(1) 台風の中心点のQ地点からP地点への移動時間は
225/30=7.5時間。
(2) よしお君の家から台風の進路予想線の最短地点が
P地点ということは∠SPQ=90度。
(3) よしお君の家が暴風域を完全にぬける時の台風の
中心点をR地点とすると、三角形PRSはPS=45km、
SR=75kmかつ∠SPR=90度の直角三角形である。
従ってPR=60kmである。(三角形PRSは3:4:5の
直角三角形)
(4) PR=60kmなので60/30=2時間でPからRまで台風の
中心点は移動する。
(5) 従って(1)の7.5時間と(4)の2時間を足した9時間
30分、即ち午前0時から9時間30分後の午前9時30分
によしお君の家は暴風域を完全にぬける。
<日本酒 さんより>
暴風域を抜けるのはQがPを超えてQS=75となるときなので、△SPQで三平方の定理よりPQ=60となりました。
よって現在の地点から285キロ地点なので9:30が答えでしょう。
<宮 さんより>
P地点が台風の暴風域に接するのが(225-75)÷30 = 5時間後。そしてP地点が暴風域から抜けそうな位置が、暴風域に接してから150÷30=5時間後。S地点はP地点が暴風域から抜ける前に抜けるので、それが何時間前なのかを求める。
S地点が暴風域を抜ける前に必ずSが暴風域の円周上にくることがある。円周上にあるS地点とP地点と暴風域の中心を結び正三角形を作る。そうすると、S地点と暴風域の中心が75、s地点とP地点が45となる。75と45は、1の位が5なので5の倍数とわかる。
さらに、それぞれ1の位と10の位を足す。すると、7+5=12、4+5=9となり、どちらも3で割り切れることから3の倍数でもある。よってこれら
は15の倍数である。これより2つの数を簡単な比に直すと、5:3となることがわかる。
だから、この三角形は5:4:3の正三角形である。よって、暴風域の中心とP地点の距離は、4×15=60。半径から60を引くと、15になる。台風が15進む時間を計算してP地点が暴風域から抜ける時間から引けばS地点が抜ける時間となる。
10-15÷30=9.5よって、答えは9時30分
<浜田明巳さんより>
次のようにvisualbasicで解析してもらいました。
Sub Command1_Click()
Dim dankai As Integer
Dim Px As Double
Dim Py As Double
Dim Qx As Double
Dim Qy As Double
Dim Sx As Double
Dim Sy As Double
Dim Qxx As Double
Dim Qx_max As Double
Dim Qx_min As Double
Dim Qx_min0 As Double
Dim Qx_max0 As Double
Dim PQ As Double
Dim QS As Double
Dim h As Double
Dim m As Double
Dim kizami As Double
Dim min As Double
Dim sa As Double
'
Px = 225
Py = 0
Qy = 0
Sx = 225
Sy = 45
kizami = 1
Qx_min0 = 0
Qx_max0 = Px + 75
min = 10000
Picture2.Cls
For dankai = 1 To 14
If dankai = 1 Then
Qx_min = Qx_min0
Qx_max = Qx_max0
Else
Qx_min = max2(Qxx - kizami, Qx_min0)
Qx_max = min2(Qxx + kizami, Qx_max0)
kizami = kizami * 0.1
End If
For Qx = Qx_min To Qx_max Step kizami
QS = Sqr((Sx - Qx) * (Sx - Qx) + (Sy - Qy) * (Sy - Qy))
If Px < Qx Then
sa = Abs(QS - 75)
If min > sa Then
min = sa
Qxx = Qx
End If
End If
PQ = Abs(Qx - Px)
h = Qx / 30
m = (h - Int(h)) * 60
h = Int(h)
Picture2.Cls
Picture2.Print "PQ="; PQ; "km, 時刻"; h; ":"; m;
If Px < Qx Then
Picture2.Print "(?), |QS-75|="; min; "km"
End If
Picture1.Cls
Picture1.Line (-50, 0)-(350, 0), vbBlue
If Px < Qx Then
Picture1.Line (Px, Py)-(Qxx, Qy), vbGreen
Picture1.Line -(Sx, Sy), vbGreen
Picture1.Circle (Qxx, Qy), 75, vbGreen
End If
Picture1.Line (Px, Py)-(Qx, Qy), vbBlack
Picture1.Line -(Sx, Sy), vbBlack
Picture1.Line -(Px, Py), vbRed
Picture1.Circle (Qx, Qy), 75, vbMagenta
Picture1.CurrentX = Px
Picture1.CurrentY = Py
Picture1.Print "P"
Picture1.CurrentX = Qx
Picture1.CurrentY = Qy
Picture1.Print "Q"
Picture1.CurrentX = Sx
Picture1.CurrentY = Sy
Picture1.Print "S"
Next Qx
Next dankai
Picture2.Cls
Picture2.Print "PQ="; PQ; "km, 時刻"; h; ":"; m; ", |QS-75|="; min; "km"
Picture1.Cls
Picture1.Line (-50, 0)-(350, 0), vbBlue
Picture1.Line (Px, Py)-(Qxx, Qy), vbBlack
Picture1.Line -(Sx, Sy), vbBlack
Picture1.Line -(Px, Py), vbRed
Picture1.Circle (Qx, Qy), 75, vbMagenta
Picture1.CurrentX = Px
Picture1.CurrentY = Py
Picture1.Print "P"
Picture1.CurrentX = Qxx
Picture1.CurrentY = Qy
Picture1.Print "Q"
Picture1.CurrentX = Sx
Picture1.CurrentY = Sy
Picture1.Print "S"
End Sub
<あつきパパ さんより>
ごり押し2次方程式で
(90√2-15√2t)^2+(135√2-15√2t)^2=75^2
よりt=11/2,19/2
5.5時間後に暴風域に入り9.5時間後に抜ける
<MARORINE さんより>
三平方の定理で、P地点から60km先の地点で暴風域を抜け
る。よって、(225+60)÷30=9.5
<高田一輝(姉小路) さんより>
3:4:5の三角形を利用して、その後
285/30=9+1/2
と言う式で解きました。
<ほげ さんより>
3:4:5から 60km
285÷30から出しました
<TOM さんより>
この問題は、台風の中心Qが実際に何km進んだかわかるかどうかがポイントです。この距離が計算できれば、あとは距離÷速さで時間
を求めることができるのです。
暴風域の半径は75kmですから、S地点から台風の通過線(問題図の青い線)にむけて75kmとなる線は2本ひける。
今回は暴風域が抜ける時間を聞いているので、北側に線を引き、その線と台風の通過線との交点をRとします。これは台風が点Rの地点を通過するとS地点は暴風域を通過することになります。
さて、QR間の距離を求めましょう。まず点PQ間は問題で225kmとわかっています。あとはPR間の長さですが、三平方の定理(ピタ
ゴラスの定理)(※1)をごぞんじの方はすぐに出ると思います。
△RPSに注目して、SR=75km、SP=45km、そして∠SPR=90°(※2)とわかっていますから、PR=60kmだとわかります。
したがって、PR=225+60=285kmとなります。
あとは、「時間=距離÷速さ」なので、時間=285÷30=9.5(時間)
よって9時間30分後となります。問題の図は午前0時ですから、0時
から9時間30分後となるので、答えは午前9時30分となります。
(※1)中3の最後の単元で学習する定理。直角三角形の斜辺(もっとも長い辺)をc、残り2辺をそれぞれa,bとおくと、
c^2 = a^2 + b^2
が成り立つ。この定理を知っていれば、直角三角形の3辺のうち、2辺がわかっていればもう1辺の長さを求めることができるのです。
今回はこれを利用しました。
(※2)「点と直線との距離」の場合、直線側の交点は必ず垂直に交わるようになります。
<ルート55 さんより>
求める台風の位置をRとする。
三角形RSPは直線SPが辺PQの最短であるので、角Pが直角となる直角三角形
またSP=45Km、RS=75Kmであるから三辺の比は3:4:5、ゆえにPR=60Km。
よって求める移動距離(QP+PR)は285Km。
台風の移動速度は時速30Kmだから、台風がQからRに至る時間は9時間30分。
Pにおける時刻は午前0時だから、
求める時刻は 9:30
