乽崱寧偺栤戣乿丂戞俇俀夞丂乮暯惉侾俇擭侾侾寧乯
| 丂
丂
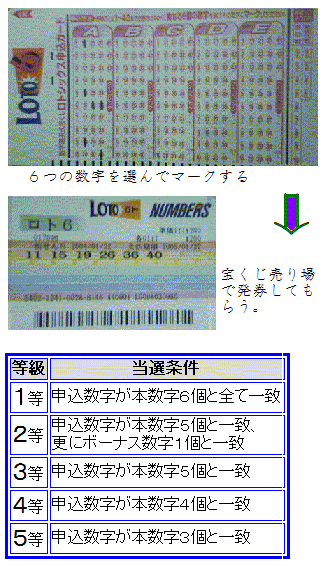
丂奆偝傫偼乽L倧倲倧俇乿偲偄偆曮偔偠傪偟偨偙偲偑偁傞偱偟傚偆偐丅Loto俇偼乽43屄偺悢帤偺拞偐傜6偮偺悢帤傪慖傃弌偡乿偲偄偆儖乕儖偺曮偔偠偱偡丅偦偺偆偪堦抳偟偨悢偑懡偗傟偽懡偄掱丄徿嬥傕崅妟偵側傞偟偔傒偱偡丅
丂僉儍儕乕僆乕僶乕偲偄偭偰摉慖幰側偟偺帪丄摉慖嬥偑師夞偵帩偪墇偝傟丄侾摍偑嵟戝係壄墌偵側傞偙偲傕偁傞偦偆偱偡丅
丂俆摍偼俇偮偺悢帤偺偆偪俁偮偺悢帤偩偗堦抳偟偨偲偒応崌偱偡丅偙偺応崌偼徿嬥偑侾侽侽侽墌偩偗傕傜偊傞偦偆偱偡丅曮偔偠偵摉偨偭偨偙偲偺側偄巹偱傕俆摍偔傜偄偼梕堈偵偁偨傝偦偆側婥偑偟傑偡
偙偙偱栤戣偱偡丅
俆摍偵側傞妋棪偼丄栺倐暘偺侾乮栺1/b乯偵側傞傛偆偱偡丅倐偵偁偰偼傑傞惍悢偼偄偔傜偵側傞偱偟傚偆偐丅
丂
丂
丂
丂
|
亙惓夝幰堦棗昞亜丂
丂丂丂丂丂丂
| 惓夝幰弴埵 |
丂丂丂丂値倎倣倕丂丂丂 |
丂丂儊乕儖摓拝擔帪丂丂 |
丂丂旛丂峫丂丂 |
| 丂侾 | Michael丂偝傫 | 2004/11/1丂0:12 | 丂 |
| 丂俀 | 帥榚將丂偝傫 | 2004/11/1丂0:13 | 惗嬵巗丂 |
| 丂俁 | 僼僕俀俈帪娫丂偝傫 | 2004/11/1丂0:13 | 崄愳導丂 |
| 丂係 | nobu丂偝傫 | 2004/11/1丂0:20 | 丂 |
| 丂俆 |
mhayashi丂偝傫 | 2004/11/1丂0:26 | 戝嶃晎丂 |
| 丂俇 | Gakkun丂偝傫 | 2004/11/1丂0:29 | 峀搰導崅峑惗僥僯晹 |
| 丂俈 | 宱桭夛偺恑嶌丂偝傫 | 2004/11/1丂0:29 | 嫗搒晎栘捗挰丒俇俇嵨丂 |
| 丂俉 |
傠傠丂偝傫 | 2004/11/1丂0:43 | 恄撧愳導丂 |
| 丂俋 | 墱擖悾丂偝傫 | 2004/11/1丂1:21 | 搶嫗搒丂 |
| 侾侽 | 媨丂偝傫 | 2004/11/1丂9:11 | 幁帣搰導丂 |
| 侾侾 | 僑儞偲傕丂偝傫 | 2004/11/1丂10:25 | 拞妛1擭惗 恄撧愳導 |
| 侾俀 | Mr.X丂偝傫 | 2004/11/1丂10:27 | 嶳棞導栍妛峑嬑柋丂 |
| 侾俁 | teki丂偝傫 | 2004/11/1丂10:54 | 戝嶃晎丂 |
| 侾係 | kasama丂偝傫 | 2004/11/1丂11:25 | 榓壧嶳導僾儘僌儔儅丂 |
| 侾俆 | ISAMU丂偝傫 | 2004/11/1丂12:23 | 嶰廳導丂 |
| 侾俇 | 側偵傢丂偝傫 | 2004/11/1丂18:29 | 惣媨巗丂 |
| 侾俈 | N.Nishi丂偝傫 | 2004/11/1丂18:53 | 戝嶃晎丗拞妛嫵桜丂 |
| 侾俉 | oguchan1丂偝傫 | 2004/11/1丂20:52 | 壀嶳導丂 |
| 侾俋 | 偪偢丂偝傫 | 2004/11/1丂22:52 | 垽昋導丂 |
| 俀侽 | Plutonian丂偝傫 | 2004/11/1丂23:01 | 柣奅傛傝丂 |
| 俀侾 | 岼偺柌丂偝傫 | 2004/11/2丂7:52 | 媨忛導弌恎丂 |
| 俀俀 | akira丂偝傫 | 2004/11/2丂11:55 | 搶嫗丂 |
| 俀俁 |
撣丂偝傫 | 2004/11/2丂15:00 | 撣傫偱偼偄偗側偄撣偪傖傫丂 |
| 俀係 | 惓偪傖傫丂偝傫 | 2004/11/2丂20:21 | 嵅夑導丂 |
| 俀俆 | 彫椦丂徦媣丂偝傫 | 2004/11/2丂21:53 | 嶉嬍嵼廧丂 |
| 俀俇 | 墠恮撪丂偝傫 | 2004/11/2丂21:29 | 撧椙導惣晹丂 |
| 俀俈 |
乮幮乯垽抦拞墰惵擭夛媍強丂偝傫 | 2004/11/2丂15:00 | 垽抦導丄侾嵨帣偺晝丂 |
| 俀俉 | 昹揷柧枻丂偝傫 | 2004/11/11丂17:57 | 丂 |
| 俀俋 |
傎偘丂偝傫 | 2004/11/12丂14:34 | 杒偺塀傟壠丂 |
| 俁侽 | 埨妝丂偝傫 | 2004/11/16丂17:17 | 媨嶈導丂 |
| 俁侾 | 偡偰偭傉丂偝傫 | 2004/11/28丂15:05 | 丂 |
丂
摎偊偼丄俁俋偱偟偨丅
亙mhayashi偝傫丂傛傝亜
夝朄偱偡丏
C(6,3)*C(37,3)/C(43,6)佮1/39
亙墱擖悾偝傫丂傛傝亜
6俠3亊37俠3亐43俠6佮39
丂
亙僑儞偲傕丂偝傫傛傝亜
愭偢丄戣堄偱憤帠徾偼43偐傜6傪慖傇偺偱binomial(43,6)丒丒丒丒丒丒嘆
偙偙偱5摍偼3屄摉慖悢抣偼偢傟偱43-6=37屄偐傜3屄傪慖傃binomial(37,3)
3屄摉慖悢抣摉偨傝偱6屄偐傜3屄傪慖傃binomial(6,3)
傛傝5摍偺帠徾偼binomial(37,3)*binomial(6,3)
偙傟偲嘆偲傛傝
binomial(37,3)*binomial(6,3)/binomial(43,6)=11100/435461
偙偙偱戣堄偱偼偙傟傪1/b(=惍悢)偱昞偡偺偱
1/(b+1)亙11100/435461亙1/b
偙偺晄摍幃偺塃曈傛傝
b亙435461/11100=39.2307丒丒丒,丒丒丒丒丒丒嘇
嵍曈傛傝
435461/11100亙b+1
38.2307丒丒丒=435461/11100-1亙b
偙傟偲嘇偲傛傝b=39丒丒丒丒丒丒(摎偊)
亙teki偝傫丂傛傝亜
乮俇亊俆亊係乛俁亊俀亊侾乯亊俇亊俆亊係亊俁俈亊俁俇亊俁俆
乛乮係俁亊係俀亊係侾亊係侽亊俁俋亊俁俉乯
亙Mr.X丂偝傫傛傝亜
俇俠俁丒(6/43)(5/42)(4/41)(37/40)(36/39)(35/38)
=栺俁俋暘偺侾
亙宱桭夛偺恑嶌丂偝傫傛傝亜
乮侾乯愭偢1乣43偐傜6屄傪慖傇乽応崌偺悢乿傪媮傔傞丅
丂丂43俠6丂傛傝丂6096454丂捠傝丅
乮俀乯5摍偼6屄偺悢帤偺偆偪3偮偺悢帤偩偗堦抳偟偨傕偺
丂丂側偺偱丂6俠3亖20丂傛傝丂20捠傝偺慻傒崌傢偣偑偁傝丄
丂丂偦偺20捠傝偺慻傒崌傢偣偵懳偟丄晇乆37俠3亖7770傛傝
丂丂7770捠傝偺慻傒崌傢偣偑偁傞丅
乮俁乯廬偭偰丄5摍偺慻傒崌傢偣憤悢偼20*7770亖155400捠傝丅
乮係乯憤悢偼丂6096454丂捠傝側偺偱丄5摍偺摉慖妋棪偼
丂丂155400/6096454亖栺1/39偱偁傞丅
乮俆乯媮傔傞倐偺抣偼39丅丂
亙彫椦丂徦媣丂偝傫傛傝亜
係俁屄偺偆偪偐傜俇屄傪慖傇慻傒崌傢偣偼俇侽俋俇係俆係捠傝偱偦偺偆
偪忦審傪枮偨偡偺偼侾俆俆係侽侽捠傝側偺偱妋棪偼侾俆俆係侽侽乛俇侽
俋俇係俆係丂傛偭偰栺侾乛俁俋
丂
亙昹揷柧枻偝傫傛傝亜
愄偺俢俷俽儅僔儞傪堷偭傁傝弌偟偰夝偒傑偟偨丏愄夰偐偟偄俶俉俉俛俙俽俬俠偱偡丏偡傋偰偺応崌傪寁嶼偟偰妋棪傪媮傔傟偽堦斣偄偄偺偱偡偑丆帪娫偑偐偐傝傑偡丏偦偙偱丆棎悢傪巊偄丆揔摉側帋峴夞悢乮侾侽侽侽侽侽夞乯偱寁嶼偟偰傒傑偟偨丏摎偼倐佮俁俋偺傛偆偱偡丏
100 'SAVE "M0411_2.BAS",A
110 RANDOMIZE VAL(RIGHT$(TIME$,2))
120 DIM A(6):MAX=43:SHIKOUKAISUU=100000!
130 BUNSHI=0
140 FOR KAISUU=1 TO SHIKOUKAISUU
150 FOR J=1 TO 6
160 ONAJI=1
170 WHILE ONAJI
180 A(J)=INT(RND*MAX)+1
190 ONAJI=0:JJ=1
200 WHILE ONAJI=0 AND JJ<J
210 ONAJI=-(A(JJ)=A(J))
220 JJ=JJ+1
230 WEND
240 WEND
250 NEXT J
260 ATARI=0:J=1
270 WHILE ATARI<=3 AND J<=6
280 ATARI=ATARI-(A(J)<=6)'1偐傜6傪摉偨傝偲偡傞
290 J=J+1
300 WEND
310 BUNSHI=BUNSHI-(ATARI=3)
320 LOCATE 0,0
330 PRINT USING "####### /####### =##.#######";BUNSHI,KAISUU,BUNSHI/KAISUU
340 ON -(BUNSHI=0) GOTO 370
350 B=KAISUU/BUNSHI:BB=INT(B+.5)
360 PRINT USING "
-> b =####.####### ->#### ?";B,BB
370 NEXT KAISUU
380 OPEN "M0411.DAT" FOR OUTPUT AS #1
390 WRITE #1,B,BB,SHIKOUKAISUU
400 CLOSE #1
410 END
