乽崱寧偺栤戣乿丂戞俇俆夞丂乮暯惉侾俈擭俀寧乯
|
|
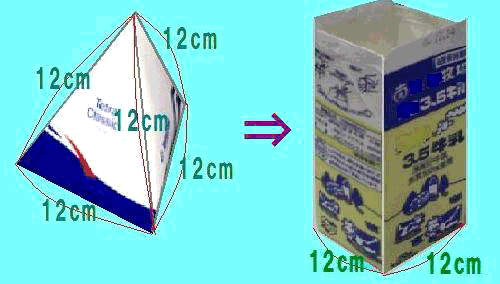
丂妛峑媼怘偱弌偝傟偨乽僥僩儔僷僢僋乮嶰妏僷僢僋乯乿偺媿擕傪抦偭偰偄傑偡偐丠丂偦偺媿擕偺僥僩儔僷僢僋偑徚柵偺婋婡偵偝傜偝傟偰偄傞偦偆偱偡丅
丂嵍恾偺傛偆偵堦曈偑侾俀cm偺惓巐柺懱偺宍傪偟偨嶰妏僷僢僋偵媿擕偑寗娫側偔擖偭偰偄傞偲偟傑偡丅
丂偙偺嶰妏僷僢僋偺媿擕傪丄堦曈偑侾俀cm偺惓巐妏拰偺宍傪偟偨媿擕僷僢僋偵堏偟曄偊傑偡丅
丂偙偙偱栤戣偱偡丅堏偟曄偊偨屻偺媿擕偺崅偝偼壗cm偵側傞偱偟傚偆偐丅
仸偨偩偟丄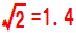 乮儖乕僩俀亖1.4乯偺嬤帡抣傪梡偄偰壓偝偄丅 乮儖乕僩俀亖1.4乯偺嬤帡抣傪梡偄偰壓偝偄丅
丂傑偨丄僷僢僋偺巻偺岤偝偼側偄偲偟傑偡丅
丂
|
亙惓夝幰堦棗昞亜丂
丂丂丂丂丂
| 惓夝幰弴埵 |
丂丂丂丂値倎倣倕丂丂丂 |
丂丂儊乕儖摓拝擔帪丂丂 |
丂丂旛丂峫丂丂 |
| 丂侾 | 嵅摗 峀愰丂偝傫 | 2005/2/1丂0:01 | 丂 |
| 丂俀 | N.Nishi丂偝傫 | 2005/2/1丂0:08 | 戝嶃晎丗拞妛嫵桜丂 |
| 丂俁 | Michael丂偝傫 | 2005/2/1丂0:09 | 丂 |
| 丂係 | y.kobayashi丂偝傫 | 2005/2/1丂0:10 | 丂 |
| 丂俆 |
傠傠丂偝傫 | 2005/2/1丂0:17 | 恄撧愳導丂 |
| 丂俇 | 側偵傢丂偝傫 | 2005/2/1丂0:19 | 惣媨巗丂 |
| 丂俈 | 摗杮屽丂偝傫 | 2005/2/1丂0:19 | 戝嶃晎抮揷巗丒23嵥丒懖榑偱朲偟偄 |
| 丂俉 | 僑儞偲傕丂偝傫 | 2005/2/1丂0:24 | 丂 |
| 丂俋 | 帥榚將丂偝傫 | 2005/2/1丂0:38 | 惗嬵巗丂 |
| 侾侽 | nobu丂偝傫 | 2005/2/1丂0:51 | 愇愳導丂 |
| 侾侾 | 宱桭夛偺恑嶌丂偝傫 | 2005/2/1丂7:06 | 嫗搒晎栘捗挰丒俇俇嵨丂 |
| 侾俀 |
僇僢僷偺撣偪傖傫丂偝傫 | 2005/2/1丂9:17 | 偨偩偺僇僢僷偱庰 |
| 侾俁 | 墱擖悾丂偝傫 | 2005/2/1丂10:09 | 搶嫗搒丂 |
| 侾係 | 岼偺柌丂偝傫 | 2005/2/1丂11:57 | 丂 |
| 侾俆 | 擔杮庰only丂偝傫 | 2005/2/1丂13:00 | 丂 |
| 侾俇 | 桬悈丂偝傫 | 2005/2/1丂23:21 | 崅抦導搚嵅嶳揷挰丂 |
| 侾俈 | Plutonian丂偝傫 | 2005/2/2丂1:08 | 柣奅傛傝丂 |
| 侾俉 |
側偐丂偝傫 | 2005/2/2丂8:06 | 杒奀摴 |
| 侾俋 | 昹揷柧枻丂偝傫 | 2005/2/2丂13:20 | 丂 |
| 俀侽 | kasama丂偝傫 | 2005/2/2丂13:26 | 榓壧嶳導僾儘僌儔儅丂 |
| 俀侾 | 埨妝丂偝傫 | 2005/2/2丂15:28 | 丂 |
| 俀俀 | akira丂偝傫 | 2005/2/2丂18:40 | 搶嫗搒丂 |
| 俀俁 | YOU丂偝傫 | 2005/2/2丂22:49 | 丂 |
| 俀係 | 偍偐丂偝傫 | 2005/2/3丂17:08 | 恄撧愳導拞妛惗 |
| 俀俆 | 側偍偭偪丂偝傫 | 2005/2/3丂20:57 | 嵅夑導丂崅峑惗 |
| 俀俇 | 僾儘價乕儉丂偝傫 | 2005/2/4丂1:22 | 嶉嬍導孎扟巗 |
| 俀俈 | 怮傞朧庡丂偝傫 | 2005/2/4丂22:17 | 丂 |
| 俀俉 | 僇僄丂偝傫 | 2005/2/5丂10:20 | 愮梩導 |
| 俀俋 | 媨丂偝傫 | 2005/2/5丂15:23 | 幁帣搰導 |
| 俁侽 | masa丂偝傫 | 2005/2/7丂0:31 | 嶳岥導 |
| 俁侾 |
崅揷堦婸丂偝傫 | 2005/2/7丂1:59 | 垽抦導嵼廧偺拞妛惗 |
| 俁俀 | 壃栰嵷曚丂偝傫 | 2005/2/8丂14:08 | 垽抦導柤屆壆巗 |
| 俁俁 |
傎偘丂偝傫 | 2005/2/9丂19:19 | 杒偺塀傟壠 |
| 俁係 |
偁偮偒僷僷丂偝傫 | 2005/2/10丂22:15 | 垽抦導丄侾嵨帣偲侽嵨帣偺晝 |
| 俁俆 | 偪偢丂偝傫 | 2005/2/12丂22:35 | 丂 |
| 俁俇 | 僋儅乕僟儞丂偝傫 | 2005/2/13丂14:43 | 暉搰導 |
| 俁俈 | oguchan1丂偝傫 | 2005/2/13丂20:12 | 壀嶳導 |
| 俁俉 | 抾拞俁擭10斣丂偝傫 | 2005/2/14丂15:42 | 抾栰挰 |
| 俁俋 | 僼僕俀俈帪娫丂偝傫 | 2005/2/16丂5:17 | 崄愳導 |
| 係侽 | 彫俇!!!乮儅僕偱乯揝摴傾僯儅儖丂偝傫 | 2005/2/16丂17:28 | 彫妛俇擭惗乮搶嫗搒乯 |
| 係侾 | 僆僇儉儔僗僩丂偝傫 | 2005/2/16丂22:47 | 嶉嬍導孎扟巗 |
| 係俀 |
傒偺偍偠丂偝傫 | 2005/2/20丂13:56 | 傉偪愭惗 |
| 係俁 | una丂偝傫 | 2005/2/23丂14:53 | 搶嫗 |
| 係係 |
nakka丂偝傫 | 2005/2/24丂0:42 | 屄暿巜摫弇島巘 |
| 係俆 | 偡偰偭傉丂偝傫 | 2005/2/27丂7:15 | 丂 |
惓夝偼丄侾丏係們倣偱偟偨丅
師偺傛偆側慺揋側夝摎傪宖帵斅偵彂偄偰偄偨偩偒傑偟偨丅
亙僑儞偲傕丂偝傫傛傝丗2005/02/01(Tue) 00:24亜
彫偝偄偱偡偹丅偱偰偨偺偵傗傝側偍偟傑偟偨丅
埲壓帺暘側傝偺夞摎偱偡丅
愭偢丄戣堄偺僥僩儔僷僢僋偺掙柺愊偼
6*6*sqrt(3)=36*sqrt(3)丒丒丒丒丒丒嘆
崅偝偼sqrt(12^2-(6*2*sqrt(3)/3)^2)=sqrt(96)=4*sqrt(6)
偙傟偲嘆偲傛傝僥僩儔僷僢僋偺懱愊偼
expand(4*sqrt(6)*36*sqrt(3)/3)=48*sqrt(3)*sqrt(6)=144*sqrt(2)丒丒丒丒丒丒嘇
傑偨偦偆偱側偄僷僢僋偺掙柺愊偼12^2=144傛傝
偙傟偲嘇偲傛傝偦偆偱側偄僷僢僋偺崅偝
=1.4丒丒丒丒丒丒(摎偊)
丂
亙僑儞偲傕丂偝傫丗2005/02/01(Tue) 01:55亜
帺暘偼惓嶰妏宍偺柺愊偼60,30,90搙偺捈妏嶰妏宍偑2偮偱
a/2妡偗傞sqrt(3)*a/2偱a^2*sqrt(3)/4
惓巐柺懱偺捀揰偐傜悅慄傪偍傠偡偲掙柺偺廳怱偑懌偱
sqrt(3)*a/2偵2/3妡偗偰偙傟偲幬曈偑a偱
嶰暯曽偺掕棟偱sqrt(a^2-(a*sqrt(3)*2/(2*3))^2)偱崅偝偑偦偟偰懱愊偼
expand((a^2*sqrt(3)/4)*sqrt(a^2-(a*sqrt(3)*2/(2*3))^2)/3);
sqrt(2)*a**2*ABS(a)/12.0=a^3*sqrt(2)/12
丂
亙側偐丂偝傫丗2005/02/02(Wed) 08:20亜
侾曈侾俀們倣偺棫曽懱偐傜係嬿傪愗傝棊偲偟偨惓巐柺懱偺懱愊偼丄
棫曽懱偺侾/俁偮傑傝丄崅偝係們倣暘偵側傝傑偡丅
乮侾乯栤戣偺僥僩儔僷僢僋偼曈偺挿偝偑偦偺侽丏俈攞側偺偱丄
懱愊偼侽丏俈丱俁攞丅係亊侽丏俈丱俁亖侾丏俁俈俀
乮俀乯傑偨偼丄係亐俀併俀亖俀亐侽丏俈亖侾侽/俈
乮俁乯傑偨偼丄係亐俀併俀亖併俀亖侾丏係
併偵嬤帡抣傪巊偆偲丄摎偺昞尰傕偄傠偄傠偱偡丅
丂
亙帥榚將 偝傫丗2005/02/08(Tue) 01:34亜
棫曽懱偺俉偮偺捀揰偺偆偪丄曈偱宷偑傜側偄係偮偺捀揰傪奺乆傓偡傃奺柺偺懳妏慄傪捠傞傛偆偵丂巐嬿傪愗抐偡傞偲丂愗傝庢偭偨棫懱
偼丄崌摨側係屄偺嶰妏偡偄乮偙傟偼丂傂偲偮偺捀揰偵俁偮偺捈妏偑
廤傑偭偨嶰妏偡偄乯偱丂巆偭偨棫懱偼丂尦偺棫曽懱偺俇杮偺懳妏慄
偺挿偝偑摍偟偄偲偙傠偐傜丂惓巐柺懱偵側傞傫偱偡僱丅
丂尦偺棫曽懱偺侾曈偺挿偝傪侾偲偡傞偲丂偦偺懳妏慄偼併2偱偡傛偹丅丂偲偙傠偱丂偙偺愗傝庢偭偨嶰妏偡偄偺懱愊偼丂掙柺愊偑惓曽宍偺柺愊偺敿暘偱尦偺棫曽懱偺懱愊偺丂1/6丂偱偡偹丅
偲尵偆偙偲偼丂巆偭偨惓巐柺懱偺懱愊偼丂侾亅乮1/6)亊係傛傝
尦偺棫曽懱偺1/3
埲忋傛傝丂侾曈偑併2偺惓巐柺懱偺懱愊偼丂1/3
偙傟傪堦斒揑偵尵偆偲丄侾曈倎偺惓巐柺懱偺懱愊傪丂倁偲偡傞偲
丂倁丗倎^3 = 1/3 : (併2 )^3 丂傛傝
丂丂倁亖乮併2 / 12乯 亊丂倎^3丂偱偡偹丅
丂
傑偨丄儊乕儖偱傕師偺傛偆側夝摎傪捀偒傑偟偨丅
亙偁偮偒僷僷丂偝傫亜
掙曈偺嵗昗傪(0,0,0),(12,0,0),(6,6併3,0)偲偡傞偲丄
捀揰偼(6,2併3,4併6)
傛偭偰惓巐柺懱偺懱愊偼12*6併3*1/2*4併6*1/3=144併2
惓巐妏拰偺掙柺愊偼12*12=144
傛偭偰144併2亐144=併2佮1.4
亙昹揷柧枻丂偝傫亜
僥僩儔僷僢僋偺惓巐柺懱俷俙俛俠偺侾曈偺挿偝傪倎偲偡傞丏
丂捀揰俷偐傜丆懳柺偺惓嶰妏宍俙俛俠偵崀傠偟偨悅慄偺懌偼丆偦偺惓嶰妏宍俙俛俠偺廳怱俧偱偁傞丏
亙恾棯亜
丂俙偐傜俛俠偵崀傠偟偨拞慄俙俫偺挿偝偼丆惓嶰妏宍俙俛俠側偺偱丆
丂丂俙俫亖併俁乛俀亊倎
丂俙俧丗俧俫亖俀丗侾偐傜丆
丂丂俙俧亖俙俫亊俀乛俁亖併俁乛俀亊倎亊俀乛俁亖倎乛併俁
丂俷俧佦俙俫偐傜丆捈妏嶰妏宍俷俙俧偵偍偄偰丆
丂丂俷俧亖(俷俙俀亅俙俧俀)侾乛俀亖(倎俀亅倎俀乛俁)侾乛俀亖併俀乛併俁亊倎
丂屘偵惓巐柺懱俷俙俛俠偺懱愊偼丆
丂丂侾乛俁亊惓嶰妏宍俙俛俠偺柺愊亊俷俧亖侾乛俁亊(併俁乛係亊倎俀)亊(併俀乛併俁亊倎)亖併俀乛侾俀亊倎俁
丂倎亖侾俀傪戙擖偡傞偲丆
丂丂併俀乛侾俀亊侾俀俁亖併俀亊侾俀俀乮偙偙傜曈偱丆侾曈偺挿偝偑侾俀偱偁傞昁慠惈偑尒偊偰偔傞乯
丂媮傔傞媿擕僷僢僋偺惓巐妏拰偺崅偝傪倛偲偡傞偲丆惓巐妏拰偺懱愊偼丆
丂丂侾俀俀亊倛亖併俀亊侾俀俀
丂丂亪倛亖併俀佮侾.係乮cm乯
亙宱桭夛偺恑嶌丂偝傫亜
乮侾乯丗堦曈12cm偺嶰妏僷僢僋偺懱愊偼丄堦曈12亐併2=6併2cm偺棫曽懱偐傜
丂丂丂掙柺愊6併2cm亊6併2cm亊1/2=36cm丱2丄崅偝6併2cm偺巐柺懱傪4屄庢傝
丂丂丂彍偄偨傕偺偱偁傞丅廬偭偰6併2丱3乮1-2/3乯=432併2亊1/3=432亊1.4亊1/3=
丂丂丂201.6棫曽cm丅
乮俀乯丗堦曈12cm偺惓巐妏拰偺宍偺媿擕僷僢僋偱偺媮傔傞崅偝傪Xcm偲偡傞丅
乮俁乯丗12亊12亊X= 201.6側偺偱丄X= 201.6亐144=1.4丅
乮係乯丗媮傔傞摎偊偼1.4cm偱偡丅

乮儖乕僩俀亖1.4乯偺嬤帡抣傪梡偄偰壓偝偄丅