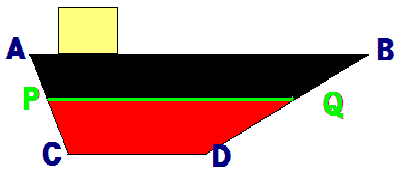
よしお君は、コンテナ船のイメージ図を書きました。
左図を見て下さい。線分ABの長さは17cm、線分CDの長さは7cmになっています。また、2つの線分は平行な位置関係です。そして、ABに平行な線分PQをひきました。
ここで問題です。赤い台形PQCDの面積と黒い台形ABPQの面積が全く同じになるとき、線分PQの長さは何cmになるでしょうか。

|
よしお君は、コンテナ船のイメージ図を書きました。 ここで問題です。赤い台形PQCDの面積と黒い台形ABPQの面積が全く同じになるとき、線分PQの長さは何cmになるでしょうか。 |
<正解者一覧表>
| 正解者順位 | name | メール到着日時 | 備 考 |
| 1 | 寺脇犬 さん | 2005/5/1 0:03 | 生駒市 |
| 2 | 呑 さん | 2005/5/1 0:04 | |
| 3 | ろろ さん | 2005/5/1 0:06 | 神奈川県 |
| 4 | ゴンとも さん | 2005/5/1 0:08 | 豊川市 |
| 5 | mhayashi さん | 2005/5/1 0:10 | 天下の台所 |
| 6 | TOMOAKI さん | 2005/5/1 0:11 | |
| 7 | N.Nishi さん | 2005/5/1 0:12 | 大阪府:中学教諭 |
| 8 | Nの悲劇 さん | 2005/5/1 0:56 | 兵庫県 |
| 9 | oguchan1 さん | 2005/5/1 1:01 | 岡山県 |
| 10 | 経友会の進作 さん | 2005/5/1 1:45 | 京都府木津町・66歳 |
| 11 | akira さん | 2005/5/1 6:50 | 東京都 |
| 12 | カエ さん | 2005/5/1 9:49 | 千葉県 |
| 13 | 藤本悟 さん | 2005/5/1 10:55 | 大阪府池田市・23才・会社やめたい |
| 14 | kasama さん | 2005/5/1 11:44 | 和歌山県プログラマ |
| 15 | 中1!!!鉄道アニマル さん | 2005/5/1 12:32 | 小学6年生(トーキョー) |
| 16 | 巷の夢 さん | 2005/5/1 13:59 | 宮城県出身 |
| 17 | いちもくa さん | 2005/5/1 15:33 | |
| 18 | 燕陣内 さん | 2005/5/1 15:38 | |
| 19 | なおっち さん | 2005/5/1 16:06 | |
| 20 | nakka さん | 2005/5/1 17:48 | 個別指導塾講師 |
| 21 | robin759 さん | 2005/5/1 18:12 | |
| 22 | なにわ さん | 2005/5/1 20:56 | 西宮市 |
| 23 | フジ27時間 さん | 2005/5/1 21:09 | 香川県 |
| 24 | masa さん | 2005/5/1 22:10 | 山口県 |
| 25 | 信三 さん | 2005/5/2 15:07 | シリコンバレーの住人 |
| 26 | nobu さん | 2005/5/2 19:22 | 石川県 |
| 27 | teki さん | 2005/5/2 23:25 | 大阪府 |
| 28 | y.kobayashi さん | 2005/5/3 0:09 | 京都府出身 |
| 29 | 高田一輝 さん | 2005/5/3 10:04 | 愛知県の中3 |
| 30 | 奥入瀬 さん | 2005/5/6 0:39 | 東京都 |
| 31 | 寝る坊主 さん | 2005/5/6 1:32 | |
| 32 | 浜田明巳 さん | 2005/5/7 16:05 | |
| 33 | スモークマン さん | 2005/5/7 18:48 | 目指せ囲碁5段! |
| 34 | kaizer さん | 2005/5/7 21:41 | 現 私立海城中学校 |
| 35 | ほげ さん | 2005/5/7 22:48 | 北の隠れ家 |
| 36 | 安楽 さん | 2005/5/9 10:08 | 宮崎県 |
| 37 | おじん さん | 2005/5/11 19:29 | 広島市 |
| 38 | 川村高雅 さん | 2005/5/12 6:00 | 神奈川県 |
| 39 | okaka さん | 2005/5/13 14:27 | 在豪社会人 |
| 40 | ウジミヤジュン さん | 2005/5/14 15:41 | |
| 41 | Michael さん | 2005/5/15 15:31 | |
| 42 | hopper さん | 2005/5/15 20:54 | 岡山県 |
| 43 | lapin さん | 2005/5/21 12:58 | |
| 44 | あつきパパ さん | 2005/5/21 18:00 | 愛知県、2歳児と0歳児の父 |
| 45 | 勇水 さん | 2005/5/22 23:15 | 高知県土佐山田町 |
| 46 | 法春 さん | 2005/5/23 15:47 | |
| 47 | おとおさん さん | 2005/5/23 16:32 | 三重県 |
| 48 | けん さん | 2005/5/27 21:17 | 長野県小布施町 |
| 49 | すてっぷ さん | 2005/5/28 8:50 |
答えは13cmでした。
投稿者:ゴンとも さん 投稿日:2005/05/01(Sun) 00:52
自分なりの解答です。
先ず、題意の図で直線AC,BDとの交点をEとし
また題意での答えであるPQ=tとして
相似な図形の面積は辺比の2乗であることを使うと
△ABE : △PQE : △DCE = 17^2(=289) : t^2 : 7^2(=49)
これと題意の図より
□APQB=△ABE-△PQE=289-t^2
□QPCD=△PQE-△CDE=t^2-49
これが題意で等しいので
289-t^2=t^2-49
この方程式を解いて
t=13・・・・・・(答え)
投稿者:tekiさん 投稿日:2005/05/02(Mon) 23:28
全く同じ問題ですね。
計算方法は
√((7^2+17^2)÷2)=13
で一発です。
経友会の進作 さんより
(1):ACの延長線とBDの延長線の交点をEとすると、三角形ABE、三角形PQE,
三角形CDEは相似形である。
(2):相似な三角形の面積比は夫々の対応する辺の二乗に比例するので、
線分PQの長さをXcmとすると、題意より17^2-X^2=X^2-7^2である。
(3):(2)を解いて、289-X^2=X^2-49より、2X^2=338、X^2=169。
(4):X>0なのでX=13。求める答えは13cmです。
高田一輝 さんより
PQ=7+x とおくと、
AP:PC=10-x:x となるので、
(7+7+x)*x/2=(17+7+x)(10-x)/2
x^2-14x-120=0
(x-6)(x+20)=0
∴x=6,-20
ここで、xは正の数より、x=6
だから、PQ=6+7=13
奥入瀬 さんより
Dを通ってACに平行な線をひき、その線とAB、PQとの交点を
それぞれE、Fとする。
□ABPQと□PQCDの高さの比を1-t:tとすると、
EB=10、FQ=10t
□PQCD=□PFCD+△FQD=7t+5t^2…①
□ABPQ=□AEPF+□EBFQ=(7-7t)+(5-5t^2)…②
①=②で、t>0より
t=3/5
よって、PQ=7+10×3/5=13
浜田明巳さんより
Visual
Basicで解きました.乱数を使い,その都度違う船を描くようにしています.
このプログラムにより,PQ=13cmである事が分かります.
Option Explicit
Const WAKU As Double = 5
Sub Form_Load()
Picture1.BackColor = vbWhite
Picture1.Scale (-WAKU, 10 + WAKU)-(17 + WAKU, -7 - WAKU)
Picture2.BackColor = vbWhite
Picture3.Picture = LoadPicture("challe_74.gif")
End Sub
Sub Command1_Click()
Randomize Timer
Dim Ax As Double
Dim Ay As Double
Dim Bx As Double
Dim By As Double
Dim Cx As Double
Dim Cy As Double
Dim Dx As Double
Dim Dy As Double
Dim Px As Double
Dim Py As Double
Dim Qx As Double
Dim Qy As Double
Dim Rx(3) As Double 'bridge
Dim Ry(3) As Double
Dim Pxx As Double
Dim Pyy As Double
Dim Qxx As Double
Dim Qyy As Double
Dim Py_max As Double
Dim Py_min As Double
Dim Py_max0 As Double
Dim Py_min0 As Double
Dim S1 As Double
Dim S2 As Double
Dim PQ As Double
Dim kizami As Double
Dim min As Double
Dim sa As Double
Dim dankai As Integer
Dim j As Integer
'
Cx = 0
Cy = 0
Dx = 7
Dy = 0
Ax = -WAKU * Rnd
Ay = 1 + WAKU * 2 * Rnd
Bx = Ax + 17
By = Ay
Rx(0) = Ax + WAKU * Rnd
Ry(0) = Ay
Rx(1) = Rx(0)
Ry(1) = Ry(0) + WAKU * Rnd
Rx(2) = Rx(1) + WAKU * Rnd
Ry(2) = Ry(1)
Rx(3) = Rx(2)
Ry(3) = Ry(0)
kizami = 0.01
Py_max0 = Ay - kizami
Py_min0 = kizami
min = 1000000
For dankai = 1 To 14
If dankai = 1 Then
Py_min = Py_min0
Py_max = Py_max0
Else
Py_min = max2(Pyy - kizami, Py_min0)
Py_max = min2(Pyy + kizami, Py_max0)
kizami = kizami * 0.1
End If
For Py = Py_min To Py_max Step kizami
Px = (Cx - Ax) / (Cy - Ay) * (Py -
Ay) + Ax
Qy = Py
Qx = (Dx - Bx) / (Dy - By) * (Qy -
By) + Bx
PQ = Qx - Px
S1 = (PQ + 17) * (Ay - Py) * 0.5
S2 = (PQ + 7) * (Py - Cy) * 0.5
sa = Abs(S1 - S2)
If min > sa Then
min = sa
Pxx = Px
Pyy = Py
Qxx = Qx
Qyy = Qy
End If
Picture2.Cls
Picture2.Print "PQ="; PQ;
"cm(?), 誤差="; min; "cm"
Picture1.Cls
Picture1.Line (Pxx, Pyy)-(Qxx, Qyy),
vbGreen
Picture1.Line (Ax, Ay)-(Cx, Cy),
vbBlack
Picture1.Line -(Dx, Dy), vbBlack
Picture1.Line -(Bx, By), vbBlack
Picture1.Line -(Ax, Ay), vbBlack
Picture1.Line (Px, Py)-(Qx, Qy),
vbGreen
Picture1.PSet (Rx(0), Ry(0)), vbBlack
For j = 1 To 3
Picture1.Line -(Rx(j),
Ry(j)), vbBlack
Next j
Picture1.CurrentX = Ax
Picture1.CurrentY = Ay
Picture1.Print "A"
Picture1.CurrentX = Bx
Picture1.CurrentY = By
Picture1.Print "B"
Picture1.CurrentX = Cx
Picture1.CurrentY = Cy
Picture1.Print "C"
Picture1.CurrentX = Dx
Picture1.CurrentY = Dy
Picture1.Print "D"
Picture1.CurrentX = Px
Picture1.CurrentY = Py
Picture1.Print "P"
Picture1.CurrentX = Qx
Picture1.CurrentY = Qy
Picture1.Print "Q"
Next Py
Next dankai
Picture2.Cls
Picture2.Print "PQ="; PQ; "cm, 誤差=";
min; "cm"
Picture1.Cls
Picture1.Line (Ax, Ay)-(Cx, Cy), vbBlack
Picture1.Line -(Dx, Dy), vbBlack
Picture1.Line -(Bx, By), vbBlack
Picture1.Line -(Ax, Ay), vbBlack
Picture1.Line (Pxx, Pyy)-(Qxx, Qyy), vbGreen
Picture1.PSet (Rx(0), Ry(0)), vbBlack
For j = 1 To 3
Picture1.Line -(Rx(j), Ry(j)), vbBlack
Next j
Picture1.CurrentX = Ax
Picture1.CurrentY = Ay
Picture1.Print "A"
Picture1.CurrentX = Bx
Picture1.CurrentY = By
Picture1.Print "B"
Picture1.CurrentX = Cx
Picture1.CurrentY = Cy
Picture1.Print "C"
Picture1.CurrentX = Dx
Picture1.CurrentY = Dy
Picture1.Print "D"
Picture1.CurrentX = Pxx
Picture1.CurrentY = Pyy
Picture1.Print "P"
Picture1.CurrentX = Qxx
Picture1.CurrentY = Qyy
Picture1.Print "Q"
End Sub
Sub Command2_Click()
Unload Me
End Sub
Private Function max2(ByVal x As Double, ByVal y As Double) As Double
If x > y Then
max2 = x
Else
max2 = y
End If
End Function
Private Function min2(ByVal x As Double, ByVal y As Double) As Double
If x < y Then
min2 = x
Else
min2 = y
End If
End Function
スモークマンさんより
x^2-7^2=17^2-x^2
2x^2=17^2+7^2=338
x^2=169=13^2
x=13
おじん さんより
まず、タンカーの図形を変形する
∠BACが直角になるように、直線ACを延長する
その延長線の直線にABと同じ長さの点をEとする
直線AE上にCEが7cmになるように点Cを、
直線ABに平行にCD、
直線ACの上に点P、直線ABに平行に直線PQ、
点Dから直線ABに垂線を引き、直線PQとの交点をRとする
題意より明らかに、CD=CE=PR=7cm
AC=FB=10cm
PC=RQ=RD=?cm
求めるPQ=PR+RQ=7+?cm
ここで台形ABCDの面積は(単位は省略)、
(AB+CD)xAC/2=(7+10+7)X10/2=120
求める面積(=2等分する面積)は60
台形PQCD=四角形PRCD+直角形RQD
PCを6cmとすると、面積は、
7x6+6x6/2=42+18=60
従って求める長さPQ=7+6=13cm
okaka さんより
求めたい値をxとし、高さをそのときの高さを、h1、h2とする。
それぞれの面積は、(7+17)(h1+h2)*1/2*1/2なので、
(7+x)*h1*1/2=(7+17)(h1+h2)*1/2*1/2
(x+17)*h2*1/2=(7+17)(h1+h2)*1/2*1/2
から、連立させて、
x=13