「今月の問題」 第75回 (平成17年12月)
|
|
<問題>
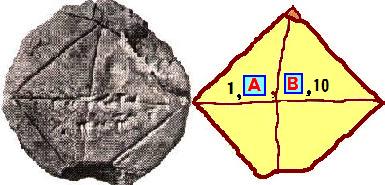
左図は古代バビロニア時代の粘土板を解読したものです。正方形の対角線には、4つの自然数、1、A、B、10が書かれています。
そして、この数字は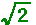 を表していることが分かりました。 を表していることが分かりました。
つまり、1+A/60+B/602+10/603
≒1.4142129・・・
≒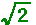
になっているようです。
ここで問題です。
Aにあてはまる数とBにあてはまる数の和、
つまり(A+B)の値はいくらになるでしょうか。
※ (A+B)の値が複数考えられる時は、その中で一番小さい数 字を答えて下さい。
|
|
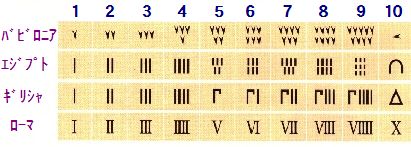
<バビロニアの数学>
左図は、古代のいろいろな数字を集めたものです。これらを比べると何か共通性も見られます。今回は、古代バビロニアの粘土板に記述されている数字に秘密を紹介しました。
今から約4000年前には、60進法の表示の仕方と正方形の対角線が一辺の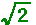 倍であることが知られていたとは驚きです。 倍であることが知られていたとは驚きです。
|
<正解者一覧表>
| 正解者順位 |
name |
メール到着日時 |
備 考 |
| 1 | teki さん | 2005/12/1 0:04 | 大阪府 |
| 2 |
nakka さん | 2005/12/1 0:06 | 個別指導塾講師@東京 |
| 3 |
mhayashi さん | 2005/12/1 0:12 | 天下の台所 |
| 4 | 寺脇犬 さん | 2005/12/1 0:17 | |
| 5 | Michael さん | 2005/12/1 0:17 | |
| 6 | 経友会の進作 さん | 2005/12/1 0:44 | 京都府木津町・67歳 |
| 7 | なにわ さん | 2005/12/1 1:53 | 西宮市 |
| 8 | 信三 さん | 2005/12/1 2:17 | シリコンバレーの住人 |
| 9 | fisherman さん | 2005/12/1 2:31 | 豊岡市 |
| 10 | ゴンとも さん | 2005/12/1 3:09 | |
| 11 | akira さん | 2005/12/1 7:58 | 東京都 |
| 12 | 翔 さん | 2005/12/1 9:52 | |
| 13 | まゆみ さん | 2005/12/1 12:35 | モルディブ在住 |
| 14 | おとおさん さん | 2005/12/1 13:05 | 三重 |
| 15 | kasama さん | 2005/12/1 14:42 | 和歌山県プログラマ |
| 16 | 浜田 明巳 さん | 2005/12/1 16:40 | |
| 17 | いちもく さん | 2005/12/1 17:48 | 七進法で110歳 |
| 18 | nobu さん | 2005/12/1 20:06 | 石川県 |
| 19 | 京都市の走る同業者 さん | 2005/12/1 21:25 | |
| 20 | いさみ さん | 2005/12/1 21:32 | 高知県香美郡 |
| 21 | oguchan1 さん | 2005/12/1 22:16 | 岡山県 |
| 22 |
お馬鹿の呑ちゃん さん | 2005/12/1 22:20 | 河童ランドの呑んだくれ |
| 23 | スモークマン さん | 2005/12/2 1:03 | 目指せ囲碁5段! |
| 24 | カエ さん | 2005/12/2 10:23 | 千葉県 |
| 25 | 巷の夢 さん | 2005/12/2 18:51 | 宮城県出身 |
| 26 | 翔鶴 さん | 2005/12/2 20:12 | ネーピア数が好きです。 |
| 27 | lapin さん | 2005/12/13 21:02 | 大阪府交野市 |
| 28 | 日本酒only さん | 2005/12/16 15:51 | |
| 29 | y.kobayashi さん | 2005/12/16 21:17 | 埼玉といえばスーパーアリーナ |
| 30 | 川村高雅 さん | 2005/12/19 13:36 | 横浜市 |
| 31 | テ さん | 2005/12/25 20:24 | 三重県 |
| 32 | 風岡 智之 さん | 2005/12/26 17:26 | |
| 33 | HPGL さん | 2005/12/28 12:20 | 愛知県、機械の開発 |
| 34 | ふじも さん | 2005/12/29 17:41 | 大阪府池田市 |
| 35 | すてっぷす さん | 2005/12/31 23:08 | 大阪府池田市 |
答えは、75でした。
teki さんの解答 投稿日:2005/12/01(Thu) 00:07 [返信]
√2=1.141421356・・・・
なので、0.141421356・・・・×60=24.8528・・・・
0.8528・・・・×60=51.1688・・・
で、A=24,B=51
ゴンともさんの解答 PART1 投稿日:2005/12/01(Thu)
03:01 [返信]
A,Bも正なのでA=25でSQRT(2)を超えているので
A=23以下ではないような気もしますが
A=24,B=51とした値も
////////1.414212962962963・・・で
SQRT(2)=1.414213562373095・・・とは
少数点以下5桁までしか一致してないので
今から調べたいところですがもう午前3時で・・・
先ず、題意での1+A/60+B/60^2+10/60^3でB/60^2の項を除き
1+A/60+10/60^3でA=24,25とするとそれぞれの値は
float(1+24/60+10/60^3);1.400046296296296・・・ ・・・・・・①
float(1+25/60+10/60^3);1.416712962962963・・・
この2近似値と題意で√2≒1.4142129・・・ ・・・・・・② よりAは25以上では不可
①,②より√2≒1.4142129-1.4000462=0.0141667
これがB/60^2よりB/60^2=0.0141667 この方程式を解いて
B=51.00012073892221
ここでBは整数だからB=51として
float(1+24/60+51/60^2+10/60^3);1.414212962962963・・・で成り立つ
よりA=24,B=51でA+B=24+51=75
この75を下まわる値はA/60とB/60^2では同じ値にするのにBはAの60倍なので
75をすべて超えて不可
よりA+B=75・・・・・・(答え)
ゴンともさんの解答 PART2 投稿日:2005/12/01(Thu)
04:26 [返信]
>A=23以下ではないような気もしますが
以下のプログラムで
Aの値が1あがるごとにBの値が60下っているという規則があり
すべての値は
float(1+1/60+1431/60^2+10/60^3);1.414212962962963で
for a=1 to 24
for b=1 to 1432
let x=1+a/60+b/60^2+10/60^3
let c=truncate(x,1)*10-truncate(x,0)*10
let d=truncate(x,2)*100-truncate(x,1)*100
let e=truncate(x,3)*1000-truncate(x,2)*1000
let f=truncate(x,4)*10000-truncate(x,3)*10000
let g=truncate(x,5)*100000-truncate(x,4)*100000
if c=4 and d=1 and e=4 and f=2 and g=1 then print a;b
next b
next a
end
a=1 b=1431 /2 1371 /3 1311 /4 1251 /5 1191
6 1131 /7 1071 /8 1011 /9 951 /10 891
11 831 /12 771 /13 711 /14 651 /15 591
16 531 /17 471 /18 411 /19 351 /20 291
21 231 /22 171 /23 111 /24 51
同様なプログラムで6桁(1.414213)まで一致するものはありませんでした。
メールでも頂きました。
経友会の進作 さんの解答
(1):題意より、1+A/60+B/3600+10/216000=1.4142129。
(2):上の式を計算すると、360*A+6*B=8946となる。
(3):上の式を満足する(A,B)は、A=1・・・・・・24とあり、
Bもそれに対応して存在する。
(4):求められているものは(A+B)の最小値でそれは、
A=24、B=51の時で、二数の和は75である。
答え:75。
浜田明巳さんの解答
A,Bは共に1以上59以下としてよいだろう.その範囲で,エクセルのマクロで解いてみる.誤差|√2-(1+A/60+B/60^2+10/60^3)|が0.0001未満になるものをすべて表示すると,
A=24,B=51
のただ1組となるので,これが答である.
このときの誤差は,
0.00000059941
である.
Option Explicit
Sub Macro1() '差が10^(-6)未満
Sheets("Sheet1").Select
Cells(1, 1).Value = 0
Range("A1").Select
Dim A As Integer
Dim B As Integer
Dim sa As Double
Dim gosa As Double
gosa = 0.0001
For A = 1 To 59
For B = 1 To 59
sa = Abs(Sqr(2) - (1 + A / 60 + B /
60 / 60 + 10 / 60 / 60 / 60))
If gosa > sa Then
Cells(1, 1).Value =
Cells(1, 1).Value + 1
Cells(Cells(1, 1).Value,
2).Value = A
Cells(Cells(1, 1).Value,
3).Value = B
Cells(Cells(1, 1).Value,
4).Value = sa
End If
Next B
Next A
End Sub
(別解)
√2の値から小数部分を取り出し,60倍して,整数部分を表示する.これを次々に繰り返すことにより,√2を60進法で表す事が出来る.この考えに基づき,次のマクロでも求めてみた.これにより,
√2=(01).(24)(51)(10)(07)(46)(06)(04)(44)(51)(36)(15)(39)(21)(31)(37)(38)(28)(20)(27)...
となる.
Option Explicit
Sub Macro3()
Sheets("Sheet3").Select
Cells(1, 1).Value = 0
Range("A1").Select
Dim a As Double
Dim j As Integer
a = Sqr(2)
For j = 1 To 20
Cells(1, j).Value = Int(a)
Cells(2, j).Value = a
a = (a - Int(a)) * 60
Next j
End Sub
スモークマンさんの解答
0.4142129x60^3=89469.9864
10+60A+3600B=89470
から、B が一番大きい数で満たすものを求めました。
ちなみに、89470/60^3=0.41421296
翔鶴 さんの解答
√2=1.4142135… である。
今、題意より、
√2=1+A/60+B/60^2+10/60^3 である。
よって、√2-1=0.4142135… であることより、
これを越えない最大の整数がAであるから、
0.40≦A/60<0.42 ⇔ 24≦A<25.2
よって、A=24,25 であるが、
A=24のとき、A/60=0.4<0.4142135…
A=25のとき、A/60=0.4166…>0.4142135… より、
A=24 は条件を満たす。
よって、1+A/60=1.4 となり、
√2-(1+A/60)=0.0142135… であることより、
これを越えない最大の整数がBであるから、
0.0140≦B/60^2<0.0143 ⇔ 50.4≦B<51.48
となり、B=51 のみ。
このとき、B/60^2=0.014166…<0.0142135…
となり、B=51 は条件を満たす。
さて、
1+A/60+B/60^2+10/60^3=1.41421296…<1.4142135…
であるから、これは題意を満たす。
よって、A=24, B=51 ∴ A+B=75 …(答)
テ さんの解答
1.4142129=1+(1/60)×0.4142129×60
=1+(1/60)×24.852774
=1+(1/60)×24+{1/(60×60)}×0.852774×60
=1+(1/60)×24+{1/(60×60)}×51.16644
=1+(1/60)×24+{1/(60×60)}×51+{1/(60×60×60)}×
0.16644×60
=1+(1/60)×24+{1/(60×60)}×51+{1/(60×60×60)}×
9.9864
=1+(1/60)×24+{1/(60×60)}×51+{1/(60×60×60)}×
(10-0.0136)
=1+(1/60)×24+{1/(60×60)}×51+{1/(60×60×60)}×
10-{1/(60×60×60)}×0.0136
ここで検算を行う
1+(1/60)×24+{1/(60×60)}×51+{1/(60×60×60)}×10
=1+0.4+0.014166666+0.000046296
=1.414212968
したがって 1+(1/60)×A+{1/(60×60)}×B+{1/(60×60×60)}×10
のA=24, B=51
としても、上の式の値は小数第7位の9までの数字に変わりはない。
だから A+B=75
風岡 智之さんの解答
A/60+B/3600+10/216000=0.4142129・・・① とおいて整理すると
60A+B=1490.999
ここでA,Bは自然数であるから
60A+B=1490 or 1491
i)60A+B=1490のとき A+Bが最小となるA,Bの組は
(A,B)=(24,50)
このとき①式は ①=1.413935
ii)60A+B=1491のとき
同様の(A,B)の組は(A,B)=(24,51)
このとき①式は ①=1.414213
となりほぼ題意に一致する。従ってA+B=75を得る

を表していることが分かりました。

倍であることが知られていたとは驚きです。