「今月の問題」 第77回 (平成18年2月)
|
<17段めの秘密>
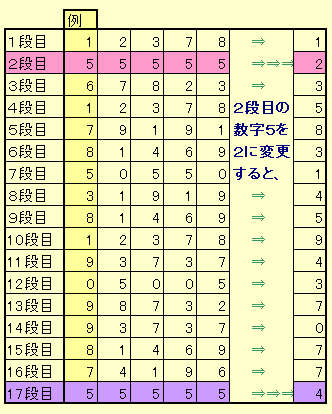
左の表の左端の列を見てください。17段のマス目に約束を決めて数字を記入したものです。
1段目の1は自由に数字を入れたものです。そして、2段目の数字は5と指定した数字を入れています。
その後、1段目の数字と2段目の数字の和6を3段目のマスに入れます。さらに、2段目と3段目の和は5+6=11となりますが、十の位は省いて1のみを書きます。このようにして、17段目まで記入したものです。
こうして、2段目の数字と17段目の数字を比べると
、2段目が5の数字の時は、17段目の数字も必ず5になります。しかし、表の右端列のように2段目を2にすると17段目は5になりません。
ここで問題です。
2段目にどのような数字を入れても、必ず2段目と同じ数字が現れるのは、何段目でしょうか。ただし、一番小さい数字で答えてください。
|
<正解者一覧表>
| 正解者順位 |
name |
メール到着日時 |
備 考 |
| 1 | ふじも さん | 2006/2/1 0:05 | 大阪府池田市 |
| 2 | なにわ さん | 2006/2/1 0:14 | 西宮市 |
| 3 |
呑 さん | 2006/2/1 0:15 | ただのヨッパライ |
| 4 | y.okada さん | 2006/2/1 0:36 | |
| 5 |
ウラル さん | 2006/2/1 0:41 | 神奈川県横浜市在住 |
| 6 | いちもく さん | 2006/2/1 5:22 | |
| 7 | スモークマン さん | 2006/2/1 5:47 | 目指せ囲碁5段! |
| 8 | teki さん | 2006/2/1 9:08 | 大阪府 |
| 9 | akira さん | 2006/2/1 10:09 | 東京都 |
| 10 | imopy さん | 2006/2/1 15:39 | 東京 |
| 11 | 経友会の進作 さん | 2006/2/1 17:38 | 京都府木津町・67歳 |
| 12 | fisherman さん | 2006/2/1 18:08 | 豊岡市 |
| 13 | 翔鶴 さん | 2006/2/1 18:23 | |
| 14 | 巷の夢 さん | 2006/2/1 19:03 | |
| 15 | Michael さん | 2006/2/1 19:11 | |
| 16 | スモークマン さん | 2006/2/1 19:31 | |
| 17 | lapin さん | 2006/2/1 20:07 | 大阪府交野市 |
| 18 | nobu さん | 2006/2/1 22:21 | |
| 19 | ゴンとも さん | 2006/2/2 0:32 | |
| 20 | 川上智弘 さん | 2006/2/2 1:28 | 兵庫県出身 |
| 21 | kasama さん | 2006/2/2 10:12 | 和歌山県プログラマ |
| 22 | カエ さん | 2006/2/2 12:17 | 千葉県 |
| 23 | ホッパー さん | 2006/2/2 16:34 | 岡山県 |
| 24 | kobayashi さん | 2006/2/2 23:55 | |
| 25 | oguchan1 さん | 2006/2/4 0:46 | 岡山県 |
| 26 | 勇水 さん | 2006/2/4 10:06 | 高知県土佐山田町(3月から香美市) |
| 27 | 翔 さん | 2006/2/4 11:00 | |
| 28 | テ さん | 2006/2/4 18:57 | 三重県 |
| 29 | 安楽 さん | 2006/2/6 15:24 | 宮崎県 |
| 30 | 2709 さん | 2006/2/6 20:33 | 兵庫県西宮市 |
| 31 | uchinyan さん | 2006/2/7 15:01 | おじさん |
| 32 | tl さん | 2006/2/8 4:15 | |
| 33 | ぴーしゅん さん | 2006/2/8 9:11 | |
| 34 | とし さん | 2006/2/9 12:59 | |
| 35 | りーくん さん | 2006/2/10 22:07 | 埼玉県 |
| 36 |
ドリー さん | 2006/2/13 22:04 | 南の島在住 |
| 37 | 電電虫 さん | 2006/2/23 15:56 | 大阪府 |
| 38 | 信三 さん | 2006/2/27 7:15 | シリコンバレーの住人 |
答えは、62段目でした。
-
[168] Re:[166]
フィボナッチ数列の1の位について 投稿者:uchinyan
投稿日:2006/02/10(Fri) 17:55 [返信]
- >
先日、あるHPで知ったのですが、フィボナッチ数列の1の位の数字の出現回数は1周期(60回)中、以下のようになっています。
>
>
1:8回、2:4回、3:8回、4:4回、5:8回、6:4回、7:8回、8:4回、9:8回、0:4回
>
> きれいな関係ですね。
なるほど、確かにそうですね。面白い ^^/
ただ、これは、「ある程度」は、説明できますね。
下一桁の数というのは 10 で割った余りのことです。
10 = 2 * 5 に注目すると...
2 で割った余りの場合、要するに、偶数奇数の場合:
1, 1, 0, 1, 1, ...
で、周期は 3 です。しかも、3
の倍数回の中に、奇数の出現:偶数の出現 = 2:1 です。
5 で割った余りの場合:
1, 1, 2, 3, 0, 3, 3, 1, 4, 0,
4, 4, 3, 2, 0, 2, 2, 4, 1, 0,
1, 1, ...
で、周期は 20 です。しかも、0 〜 4 がすべて 4
回ずつ出現しています。
10 で割った余りの場合の周期は 60 でしたから、60 = 3 * 20
で、5 で割った余りの場合が 3 回繰り返されます。
ここで、例えば 1 を考えると、5 で割った余りの場合に 1
は 4 回出現するので、
10 で割った余りの場合には 4 * 3 = 12 回、出現します。
さらに、5 で割った余りの場合の 1 に対して、10
で割った余りの場合には 1, 6 = 1 + 5 が対応します。
ところが、奇数の出現:偶数の出現 = 2:1 なので、1 が
12 * 2/3 = 8 回、6 が 12 * 1/3 = 4 回、と分かります。
他の数字も同様になります。
要は、2 で割った余りの場合と 5
で割った余りの場合とに還元できる、ということです。
-
[167] いい頭の体操でした・・・
投稿者:経友会の進作
投稿日:2006/02/10(Fri) 08:08 [返信]
- 老化防止の一環として下一桁の数同士を加算するのがいい
ようです。僕も地道に一つずつ足していきました。そうする
と60回で一回りするのですね。これは面白い。干支も60年で
一回りします。そう、還暦が60歳ですね。60っていう数字は
不思議な数字です。uchinyanさん、tekiさん多々ご教授あり
がとうございます。
-
[166] フィボナッチ数列の1の位について
投稿者:teki
投稿日:2006/02/09(Thu) 13:13 [返信]
- 先日、あるHPで知ったのですが、フィボナッチ数列の1の位の数字の出現回数は1周期(60回)中、以下のようになっています。
1:8回、2:4回、3:8回、4:4回、5:8回、6:4回、7:8回、8:4回、9:8回、0:4回
きれいな関係ですね。
-
[165] Re:[163]
やはり、一度は、頑張って計算をするのかなぁ
投稿者:teki
投稿日:2006/02/07(Tue) 21:54 [返信]
- >
なお、フィボナッチ数列の下一桁が60周期で繰り返すことは、私も今回はじめて知りましたが、
>
覚えていていいことかもしれませんね。何か深い意味があるのかもしれない...?
フィボナッチ数列の1の位が60回周期なのは、私も始めて知りましたが、古代の人は60進法(現在の時刻、角度等も含めて)を知っていたようで、この辺にも何か偶然とは思えないものがあるような気がします。
-
[164] Re:[163]
やはり、一度は、頑張って計算をするのかなぁ
投稿者:uchinyan
投稿日:2006/02/07(Tue) 17:48 [返信]
- 済みません。
> tekiさんの[157]や2702さんの[161]&[162]と同じように考えるのがいいと思います。
「2702さん」−>「2709さん」です m(__)m
-
[163] やはり、一度は、頑張って計算をするのかなぁ
投稿者:uchinyan
投稿日:2006/02/07(Tue) 13:31 [返信]
- 通りすがりの者です。スモークマンさんに教えてもらって、初めて来ました。
やはり、一度は、60数回計算をするしかない、というか、それが一番簡単、なような気がします。
数学になってしまいますが、少しまとめておきましょう。
tekiさんの[157]や2702さんの[161]&[162]と同じように考えるのがいいと思います。
1段目を c、2段目を a とすると、n >= 3 として、
3段目:1 * c + 1 * a
4段目:1 * c + 2 * a
5段目:2 * c + 3 * a
6段目:3 * c + 5 * a
7段目:5 * c + 8 * a
...
n段目:f(n-2) * c + f(n-1) * a
の下一桁、と書けます。ただし、f(n) は、tekiさんのおっしゃっているフィボナッチ数列で、
f(1) = 1, f(2) = 1, f(n) = f(n-1) + f(n-2), n >= 3
です。具体的には、
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
n段目がこうなる理由は、今回の問題の計算の仕方とフィボナッチ数列のそれとが、
基本的に同じであることから分かると思います。
(正確には、数学的帰納法という証明方法、高校で習います、を用いて証明できます。)
さて、この後はどうしようもないと思うのですが、フィボナッチ数列の下一桁を計算していくと、
1, 1, 2, 3, 5, 8, 3, 1, 4, 5,
9, 4, 3, 7, 0, 7, 7, 4, 1, 5,
6, 1, 7, 8, 5, 3, 8, 1, 9, 0,
9, 9, 8, 7, 5, 2, 7, 9, 6, 5,
1, 6, 7, 3, 0, 3, 3, 6, 9, 5,
4, 9, 3, 2, 5, 7, 2, 9, 1, 0,
1, 1, ...(以下繰り返し)...
つまり、60周期で繰り返します。そこで、先ほどの n段目の式に
n = 62 とすると、
62段目:f(62-2) * c + f(62 - 1) * a = f(60) * c + f(61) * a =(下一桁)=
0 * c + 1 * a = a
で、62段目が 2段目に等しいことが分かります。
また、60周期なので、途中の段では、c や a
が中途半端に残ってしまうのも分かりますし、
62段目が最小なのも分かります。
ということで、62段目なのですが、却って、難しくなってしまったでしょうか...
なお、フィボナッチ数列の下一桁が60周期で繰り返すことは、私も今回はじめて知りましたが、
覚えていていいことかもしれませんね。何か深い意味があるのかもしれない...?
[161] やっと 投稿者:2709
投稿日:2006/02/06(Mon) 20:29 [返信]
- 1だんめ=A2段目=B3段目=ABとやってはじめてAが**0こBが**1個になるとき
[160] Re:[159] お初です。
投稿者:teki
投稿日:2006/02/05(Sun) 23:32 [返信]
- > わたしも初めて投稿します。
> ここは気がつかなかった〜。。。
> 結局フィボナッチなんですね!
> 面白かったですが、計算中100回以内には出るはずだからとずっと計算しましたが、、、
> もっと簡略に出せるんでしょうか?
私も、もう少し簡単に出せないか考えたんですが、結局60個目まで探しました。
どなたか、もう少し簡単に出せる方法があったら、ご教示ください。
-
[159] お初です。 投稿者:スモークマン
投稿日:2006/02/05(Sun) 17:08 [返信]
- わたしも初めて投稿します。
ここは気がつかなかった〜。。。
結局フィボナッチなんですね!
面白かったですが、計算中100回以内には出るはずだからとずっと計算しましたが、、、
もっと簡略に出せるんでしょうか?
-
[158] 初めて投稿しますが
投稿者:ホッパー 投稿日:2006/02/02(Thu) 16:26 [返信]
- 正解できたのかな?
-
[157] 今回は 投稿者:teki
投稿日:2006/02/01(Wed) 09:10 [返信]
- フィボナッチ数列の問題ですね。
連続したフィボナッチ数列の1の位が、0と1になるのは、59個目と60個目ですので、59+3=62段目は必ず2段目と同一の数字が現れます。
-
メールでも頂きました。
翔鶴 さんの解答
p,qを0≦p≦9,0≦q≦9なる整数とし、
{a(n)}を
a(1)=p,a(2)=q,
a(n+2)=a(n+1)+a(n) (n=1,2,…) …(*)
と定義する。
(*)を用いて、
a(3)=p+q,a(4)=p+2q,a(5)=2p+3q,a(6)=3p+5q,
a(7)=5p+8q,…,a(k)=b(k-1)p+b(k)q
とかける。
ただし、b(0)=0,b(1)=1,
b(n+2)=b(n+1)+b(n) (n=1,2,…) …(**)
とする。
題意より、p,qの値にかかわらず、
a(2)≡a(k) (mod10)
が成立することが必要十分。
すなわち、
a(2)-a(k)≡0 (mod10)
⇔q-b(k-1)p-b(k)q≡b(k-1)p+{b(k)-1}q≡0 (mod10)
⇔b(k-1)p+{b(k-2)+b(k-1)-1}q
=(p+q)b(k-1)+{b(k-2)-1}q≡0 (mod10)
(∵(**)より)
よって、A,B,Cを適当な整数として、
b(k-2)-1=10A,b(k-1)=10B,b(k)-1=10C
⇔b(k-2)=10A+1,b(k-1)=10B,b(k)=10C+1
とかける。このようなkが求めるものである。
以下は(**)の項の1の位のみを書いたものである。
0,1,1,2,3,5,8,3,1,4,
5,9,4,3,7,0,7,7,4,1,
5,6,1,7,8,5,3,8,1,9,
0,9,9,8,7,5,2,7,9,6,
5,1,6,7,3,0,3,3,6,9,
5,4,9,3,2,5,7,2,9,1,
0,1
以上より、求めるものは、
62…(答)
スモークマン の解答
3段目から、
(1,1),(1,2),(2,3),(3,5),(5,8),(8,3),(3,1),(1,4),(4,5),
(5,9),(9,4),(4,3),(3,7),(7,0),(0,7),(7,7),(7,4),(4,1),
(1,5),(5,6),(6,1),(1,7),(7,8),(8,5),(5,3),(3,8),(8,1),
(1,9),(9,0),(0,9),(9,9),(9,8),(8,7),(7,5),(5,2),(2,7),
(7,9),(9,6),(6,5),(5,1),(1,6),(6,7),(7,3),(3,0),(0,3),
(3,3),(3,6),(6,9),(9,5),(5,4),(4,9),(9,3),(3,2),(2,5),
(5,7),(7,2),(2,9),(9,1),(1,0),(0,1)!
つまり、2+60=62段目!
川上智弘 さんの解答
1段目の数字をa,2段目の数字をbとおくと4段目以上,aのn+1段目の1の
位とbのn段目の1の位は常に正しくなります。
2段目と常に値が等しくなるにはaの1の位が0且つbの1の位が1になる必
要があります。
それを探していくと62段目が該当します。
経友会の進作 さんの解答
ここでは、紹介できませんが、エクセルで証明していただきました。
テ さんの解答
1段目の数字をa 2段目の数字をbとすると、n段目の数字は、P ×a+Q×b と表すことが出来る。
Pは、 n−1段目の Q の値と等しい。
P、 Q の 1の位の数字をp 、q とするとき
p×a+q×bと表すことが出来る。p=0, Q=1 となるのが、何段目であるかを調べればよい。
原始的なやり方ですが、1段目から順番に、その段の数字の1の位の数字を書くと
0,1,1、2,3、・・・・、0,1・・・となり、61段
めが0で、62段目が1となるので
求める段は、62段目である。
信三 さんの解答
1, m, 1+m, 1+2m, 2+3m, 3+5m, 5+8m, 8+3m, 3+1m, 1+4m, 4+5m,
5+9m, 9+4m, 4+3m, , , ,と辿って、
第1項が 0、第2項の係数が 1になるまで行きついたら、
第62項になりました
