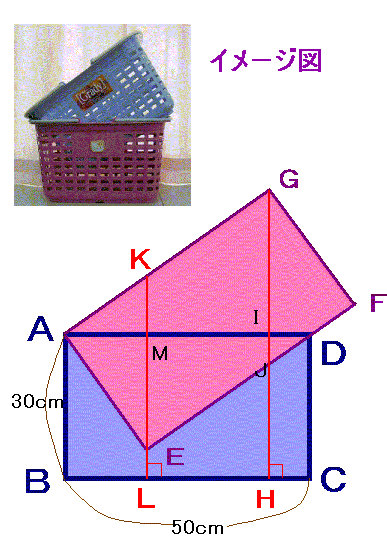
|
左のイメージ図を見てください。 この買い物かご２つを左図ののように、点Ａの１点で重ね、長方形AEFGの辺EFのどこかと長方形ABCDのD点が重なるように置いてあります。 また、長方形AEFGのＧから下ろした垂線とBCとの交点をHとします。またＥから下ろした垂線とBCとの交点をLとしAGとの交点をＫとします。 ここで問題です。ＡＢ：ＫＬ：ＧＨの線分の比を、できるだけ簡単な整数で書いてください。 |
＜正解者一覧表＞ ３月３０日 7:00 現在
| 正解者順位 | ｎａｍｅ | メール到着日時 | 備 考 |
| １ | 呑 さん | 2006/3/1 0:12 | 馬鹿なカッパで酒 |
| ２ | 2709 さん | 2006/3/1 0:14 | 兵庫県西宮市 |
| ３ | mhayashi さん | 2006/3/1 0:14 | 天下の台所 |
| ４ | なにわ さん | 2006/3/1 0:24 | 西宮市 |
| ５ | oguchan1 さん | 2006/3/1 0:46 | |
| ６ | 経友会の進作 さん | 2006/3/1 1:06 | 京都府木津町・67歳 |
| ７ | ゴンとも さん | 2006/3/1 1:13 | |
| ８ | りーくん さん | 2006/3/1 1:40 | 埼玉県 |
| ９ | ふじも さん | 2006/3/1 1:59 | 大阪府池田市 |
| １０ | いちもく さん | 2006/3/1 7:28 | |
| １１ | 巷の夢 さん | 2006/3/1 7:45 | |
| １２ | 翔鶴 さん | 2006/3/1 9:45 | 福岡 |
| １３ | 電電虫 さん | 2006/3/1 10:38 | 大阪府 |
| １４ | akira さん | 2006/3/1 13:24 | 東京都 |
| １５ | 信三 さん | 2006/3/1 15:51 | シリコンバレーの住人 |
| １６ | スモークマン さん | 2006/3/1 16:16 | 目指せ囲碁5段！ |
| １７ | テトラクテュスグラマトン さん | 2006/3/1 21:48 | |
| １８ | seiyoku さん | 2006/3/1 21:55 | |
| １９ | fisherman さん | 2006/3/1 22:36 | 豊岡市 |
| ２０ | y.kobayashi さん | 2006/3/2 2:12 | イナバウアー！！ |
| ２１ | assa さん | 2006/3/2 3:08 | 大阪府在住の大学生 |
| ２２ | tl さん | 2006/3/2 4:11 | |
| ２３ | テ さん | 2006/3/2 8:24 | 三重県 |
| ２４ | kasama さん | 2006/3/2 9:55 | 和歌山県 |
| ２５ | imopy さん | 2006/3/2 13:27 | |
| ２６ | teki さん | 2006/3/2 15:16 | 大阪府の酔っ払い |
| ２７ | uchinyan さん | 2006/3/2 18:19 | |
| ２８ | 安楽 さん | 2006/3/2 21:02 | 宮崎県 |
| ２９ | カエ さん | 2006/3/2 22:01 | 千葉県 |
| ３０ | ファルコン さん | 2006/3/3 2:07 | 宝塚市 |
| ３１ | 日本酒only さん | 2006/3/3 16:22 | 宝塚市 |
| ３２ | しゅん さん | 2006/3/3 17:24 | 野球狂 |
| ３３ | N.Nishi さん | 2006/3/5 14:30 | |
| ３４ | 京都市の走る同業者 さん | 2006/3/5 18:42 | |
| ３５ | ほげ さん | 2006/3/6 9:58 | 北の隠れ家 |
| ３６ | lapin さん | 2006/3/6 16:27 | 大阪府交野市 |
| ３７ | 秋山優貴 さん | 2006/3/6 18:42 | 滋賀県野州市中３ |
| ３８ | 開拓塾 さん | 2006/3/7 0:44 | |
| ３９ | 大学生 さん | 2006/3/7 12:26 | 埼玉県 |
| ４０ | 石原幹男 さん | 2006/3/7 15:38 | なまよみの甲斐の国盲人 |
| ４１ | 岡本ボンバーズ さん | 2006/3/10 9:21 | 秋田県 |
| ４２ | nobu さん | 2006/3/11 20:47 | 石川県 |
| ４３ | 翔 さん | 2006/3/12 17:43 | 香川県 |
| ４４ | stone さん | 2006/3/15 13:35 | |
| ４５ | マロン さん | 2006/3/15 23:08 | 入試に向けてがんばります |
| ４６ | ぴーしゅん さん | 2006/3/16 10:03 | |
| ４７ | ＨＫ さん | 2006/3/16 15:12 | 富山市寺町 |
| ４８ | CHOPELIX さん | 2006/3/17 4:18 | 茅ヶ崎市民 |
| ４９ | Michael さん | 2006/3/17 19:57 | |
| ５０ | 川上智弘 さん | 2006/3/19 16:20 | 兵庫県出身 |
| ５１ | 息子と乙女 さん | 2006/3/21 18:12 | |
| ５２ | どんぐり さん | 2006/3/25 13:15 | 神奈川県 |
| ５３ | Leon さん | 2006/3/26 14:37 | 北海道 |
| ５４ | 石井怜 さん | 2006/3/30 0:04 | 京都府京田辺市 |
答えは 20:29:40 です。
[177] センター試験に出るかも？ 投稿者：fishermamさん
投稿日：2006/03/02(Thu)
（１）三角比で出来ます。
cos∠ＤＡＥ＝３/５よりsin∠ＤＡＥ＝４/５，
tan∠ＤＡＥ＝４/３ よってＡＭ＝１８，
tan∠ＧＡＤ＝tan(90°−∠ＤＡＥ）＝１/tan∠ＤＡＥ
＝３/４ よってＫＭ＝２７/２
sin∠ＧＡＤ（90°−∠ＤＡＥ）＝cos∠ＤＡＥ＝３/５
よってＧＩ＝３０
ＡＢ：ＫＬ：ＧＨ＝30:(27/2+30):(30+30)＝20:29:40
（２）三角形の相似、合同で出来ます。
[173] 辺比3:4:5の直角三角形 投稿者：ゴンともさん
投稿日：2006/03/01(Wed)
だけでできました。
先ず、題意の答えの比は図からKM,GIを求めればわかるので
その二つを求めることにする。
KMは
△AEDがAE=30,AD=50,∠AED=90°より
△AEDは辺比3:4:5の直角三角形
また△AEMは△AEDと∠MAE,AEが共有されていてで∠AME=90°より
AE:AD=3:5=AM:30=AM:AE ∴ 5*AM=90 ∴ AM=18
これと△AMKも△AED,△AMEも辺比3:4:5の直角三角形より
AM:MK=18:MK=4:3 ∴ MK=18*3/4=27/2・・・・・・☆
GIは
△AGDも辺比3:4:5の直角三角形より
AG:GI=50:GI=5:3 ∴ AI=30・・・・・・☆☆
以上☆,☆☆より
AB:KL:GH=AB:KM+ML:GI+IH=30:30+27/2:30+30=60/2:87/2:120/2=60:87:120
=20:29:40・・・・・・(答え)
imopy さんより
AM:18cm、KM:27/2cmより、KL:87/2cm
GI:30cmより、GH:60cm
AB:KL:GH＝30:87/2:60＝60:87:120＝20:29:40
3:4:5の直角三角形が鍵ですね・・・。