乽崱寧偺栤戣乿丂戞俉侽夞丂乮暯惉侾俉擭俆寧乯

丂僑乕儖僨儞僂傿乕僋偼丄梀墍抧偺戝娤棗幵偱妝偟傓曽傕懡偄偺偱偼側偄偱偟傚偆偐丅
丂幨恀偼丄戝嶃奀梀娰偺椬偵偁傞乽揤曐嶳戝娤棗幵乿偱偡丅
丂悽奅嵟戝媺偺崅偝傪屩傞偦偆偱偡丅惏傟偨擔偵偼丄搶偼惗嬵嶳宯丄惣偼柧愇奀嫭戝嫶丄撿偼娭惣崙嵺嬻峘丄杒偼榋峛嶳宯傑偱丄偖傞偭偲堦朷偱偒傞偲徯夘偟偰偁傝傑偟偨丅
丂栭偼丄60戜偺僉儍價儞偲夞揮幉偑僀儖儈僱乕僔儑儞偵婸偒丄30暘枅偵帪曬傪抦傜偣傞懪偪忋偘壴壩偺傛偆側僔儑乕偑妝偟傔傞偦偆偱偡丅
|
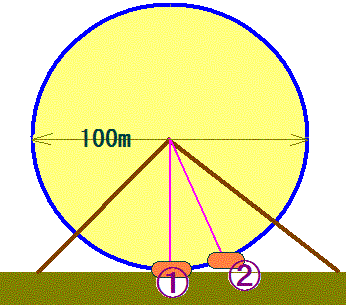
丂偙偺娤棗幵偼丄俇侽戜偺僑儞僪儔偑墌廃忋傪摍懍偱摦偄偰偄傑偡丅
丂傑偨丄偙偺僑儞僪儔偑摦偔墌廃偺捈宎偼侾侽侽倣偱偁傞偙偲偑暘偐偭偰偄傑偡丅
丂傛偟偍孨偑嵟傕掅偄埵抲偱丄嘆偺僑儞僪儔偵忔偭偨偲偒偐傜丄侾俋俆昩屻偵丄係戜愭傪摦偔僑儞僪儔嘇偑傛偟偍孨偑忔偭偰偄傞僑儞僪儔嘆偺恀忋偺埵抲偵弶傔偰偒偨偦偆偱偡丅
丂偙偙偱栤戣偱偡丅偙偺僑儞僪儔偼帪懍壗km偺懍偝偱摦偄偰偄傞偺偱偟傚偆偐丅偨偩偟丄墌廃棪偼俁丏侾係偲偟偰寁嶼傪偟偰丄彫悢偱摎偊偰壓偝偄丅
|
亙惓夝幰堦棗昞亜丂
丂丂丂丂丂丂丂丂
| 惓夝幰弴埵 |
丂丂丂丂値倎倣倕丂丂丂 |
丂丂儊乕儖摓拝擔帪丂丂 |
丂丂旛丂峫丂丂 |
| 丂侾 | teki丂偝傫 | 2006/5/1丂0:06 | 戝嶃晎丂 |
| 丂俀 | oguchan1丂偝傫 | 2006/5/1丂0:10 | 幁帣搰導丂 |
| 丂俁 | 隳丂偝傫 | 2006/5/1丂0:13 | 崄愳導丂 |
| 丂係 | 愳忋抭峅丂偝傫 | 2006/5/1丂0:23 | 暫屔導惗傑傟丂 |
| 丂俆 | 宱桭夛偺恑嶌丂偝傫 | 2006/5/1丂0:28 | 嫗搒晎栘捗挰丒67嵨丂 |
| 丂俇 | 僥丂偝傫 | 2006/5/1丂1:05 | 嶰廳導丂 |
| 丂俈 | y.kobayashi丂偝傫 | 2006/5/1丂1:29 | 嶉嬍丂 |
| 丂俉 | 偄偪傕偔丂偝傫 | 2006/5/1丂5:06 | 棫愳巗丂 |
| 丂俋 | 岼偺柌丂偝傫 | 2006/5/1丂7:38 | 丂 |
| 侾侽 | uchinyan丂偝傫 | 2006/5/1丂9:25 | 丂 |
| 侾侾 | 側傑傛傒偺栍妛峑嫵巘丂偝傫 | 2006/5/1丂14:39 | 峛斻偺崙丂 |
| 侾俀 | 昹抧丂戝夘丂偝傫 | 2006/5/1丂15:39 | 嶳忛慇堐岺嬈姅幃夛幮丂 |
| 侾俁 | 僗儌乕僋儅儞丂偝傫 | 2006/5/1丂17:34 | 栚巜偣埻岄5抜両丂 |
| 侾係 | 僇僄丂偝傫 | 2006/5/1丂18:11 | 愮梩導丂 |
| 侾俆 | 墠恮撪丂偝傫 | 2006/5/1丂21:10 | 戝嶃嵼廧丒怮晄懌丂 |
| 侾俇 | 怣嶰丂偝傫 | 2006/5/2丂9:14 | 僔儕僐儞僶儗乕偺廧恖丂 |
| 侾俈 | imopy丂偝傫 | 2006/5/2丂13:37 | 搶嫗搒丂 |
| 侾俉 | 傝乕偔傫丂偝傫 | 2006/5/2丂17:13 | 嶉嬍導丂 |
| 侾俋 | 僄僩儔儞僛丂偝傫 | 2006/5/2丂18:35 | 丂 |
| 俀侽 | CHOPELIX丂偝傫 | 2006/5/2丂20:44 | 姖儢嶈巗柉丂 |
| 俀侾 | fisherman丂偝傫 | 2006/5/2丂23:57 | 朙壀巗丂 |
| 俀俀 | 側偵傢丂偝傫 | 2006/5/3丂22:13 | 惣媨巗丂 |
| 俀俁 | ISAMU丂偝傫 | 2006/5/4丂16:41 | 嶰廳導丂 |
| 俀係 | 偡偰偭傉丂偝傫 | 2006/5/4丂22:04 | 丂 |
| 俀俆 | 隳掃丂偝傫 | 2006/5/5丂11:34 | 丂 |
| 俀俇 |
幒挰昐晎丂偝傫 | 2006/5/7丂11:17 | 搶嫗嵼廧丂 |
| 俀俈 | kasama丂偝傫 | 2006/5/10丂0:05 | 榓壧嶳導僾儘僌儔儅丂 |
| 俀俉 | 偳傫偖傝丂偝傫 | 2006/5/10丂11:52 | 恄撧愳導丂 |
| 俀俋 | 戝曘丂偝傫 | 2006/5/10丂23:15 | 丂 |
| 俁侽 |
側偐丂偝傫 | 2006/5/11丂19:44 | 杒奀摴丂 |
| 俁侾 | 傄乕偟傘傫丂偝傫 | 2006/5/12丂14:43 | 丂 |
| 俁俀 | nobu丂偝傫 | 2006/5/13丂12:05 | 愇愳導丂 |
| 俁俁 | 揹揹拵丂偝傫 | 2006/5/13丂22:53 | 戝嶃晎丂 |
| 俁係 | Michael丂偝傫 | 2006/5/22丂19:31 | 丂 |
| 俁俆 | 偁傒偂丂偝傫 | 2006/5/24丂4:02 | 丂 |
| 俁俇 | 僀僘働乕丂偝傫 | 2006/5/26丂14:50 | |
| 俁俈 |
hidy丂偝傫 | 2006/5/27丂7:42 | 暉壀導偺揷幧丂 |
| 俁俉 | 嬻攇丂偝傫 | 2006/5/28丂17:49 | 暫屔導 |
摎偊偼丄侾丏俀俆俇倠倣乛帪丂偱偟偨
丂
儊乕儖偱捀偄偨夞摎傪徯夘偝偣偰偄偨偩偒傑偡丅
亙愳忋抭峅丂偝傫傛傝亜
墌廃偺挿偝偼100亊3.14亖314儊乕僩儖丅
195昩偱偦偺314亊13/60儊乕僩儖堏摦弌棃傞偺偱
娤棗幵偺懍偝偼314/900m/昩偱偁傞丅
偙傟傪帪懍偵捈偡偲1256m/帪偱偁傞丅
傛偭偰娤棗幵偼栺1.256km/帪偺懍偝偱堏摦偟偰偄傞丅
亙僥丂偝傫傛傝亜丂
傛偟偍孨偑忔偭偨僑儞僪儔偲係戜愭偺僑儞僪儔偺妏搙偼丂丂俁俇侽亊係亐俇侽搙亖俀係搙丅
偙偺俀戜偺僑儞僪儔偼侾俋俆昩丂屻偵丂忔幵埵抲偐傜丂俋侽搙亄侾俀搙丄俋侽亅侾俀搙丂偺埵抲偵恑傓丅
偮傑傝丄僑儞僪儔偼丂侾俋俆昩偱丂俋侽亅侾俀搙丂恑傓丅捈宎丂侾侽侽m丂偺墌廃忋偺揰偑
俋侽亅侾俀搙丂恑傓偐傜丄侾俋俆昩偱丂侾侽侽亊俁丏侾係亊乮俋侽亅侾俀乯亐丂俁俇侽m丂恑傓丅
昩懍丂侾侽侽亊俁丏侾係亊乮俋侽亅侾俀乯亐丂俁俇侽丂亐侾俋俆m
偱偁傞丅帪懍丂X 倣丂偲偡傞偲
侾侽侽亊俁丏侾係亊乮俋侽亅侾俀乯亐丂俁俇侽丂亐丂侾俋俆亖丂X丂亐丂俁俇侽侽
X丂亖丂侾俀俆俇丂丂丂丂丂
偙偺僑儞僪儔偼丂帪懍丂侾俀俆俇m 偱偁傞丅
丂亙宱桭夛偺恑嶌丂偝傫傛傝亜
乮侾乯丗墌廃360搙偵摍娫妘偱60戜偺僑儞僪儔偑摦偄偰偄傞偺偱
丂丂丂丂奺僑儞僪儔偲偡偖椬傝偺僑儞僪儔偲偺妏搙嵎偼6搙丅
乮俀乯丗偙偺墌偼捈宎100倣側偺偱墌廃偺偺挿偝偼314倣丅丂丂丂丂
乮俁乯丗195昩屻偵弶傔偰4戜愭傪峴偔僑儞僪儔偑恀忋偵棃偨
丂丂丂丂偲偄偆偙偲偼丄擇偮偺僑儞僪儔偼90+12=102搙偲
丂丂丂丂90-12=78搙偺埵抲娭學偵偁傞丅偮傑傝195昩偱78搙
丂丂丂丂堏摦偟偨偙偲偵側傞丅丂丂丂丂
乮係乯丗195昩偱78搙偺堏摦偼900昩偱360搙偺堏摦側偺偱丄
丂丂丂丂900昩偱314倣丅3600昩乮1帪娫乯偱314*4=1256倣丅
丂丂丂丂媮傔傞帪懍偼1256倣/帪=1.256倠倣/帪丅
丂摎偊丗帪懍1.256倠倣丅
亙隳掃丂偝傫傛傝亜
僑儞僪儔摨巑偺娫妘偼6搙側偺偱丄
4屄愭偺僑儞僪儔傑偱24搙丅
偦傟偑恀忋偵棃傞偺偱丄195昩偱(90-12)搙=78搙
偱恑傓丅
傛偭偰丄僑儞僪儔偺摦偔懍偝偼丄
78[搙]*(3.14/180[搙])/195[昩]*50[m]*3600[昩]/1000
=1.256 [km/h]
亙幒挰昐晎丂偝傫傛傝亜
僑儞僪儔偼墌廃忋偵俇侽戜側偺偱丄俇搙偺娫妘偱暲傫偱偄傞丅
墌廃偼314倣丅4戜愭偺僑儞僪儔俀偲侾偲偼丄24搙偺嵎偑偁傞丅
恀忋偵棃傞偲偄偆偙偲偼丄墌偲偄偆惈幙忋墌偺拞怱傪捠傞悈暯慄
傪偼偝傫偱侾偲墌偺拞怱傪寢傇慄偲悈暯慄偺側偡妏偲丄俀偲墌偺
拞怱傪寢傇慄偲悈暯慄傪寢傇慄偺側偡妏偑摍偟偔側傞偲偄偆偙偲
側偺偱丄俋侽亅俀係乛俀偐傜丄侾偑俈俉搙恑傓偲俀偑恀忋偵棃傞
偙偲偵側傞丅屻偼恑傫偩嫍棧丄偐偐偭偨帪娫傪傕傠傕傠寁嶼偡傞
偲丄帪懍1.256倠倣偲側傞丅丂丂
亙偁傒偂丂偝傫傛傝亜
俁俇侽搙亐俇侽亖俇
俋侽亅俇倶俀亖俈俉
侾侽侽倶俁丏侾係倶俈俉亐俁俇侽亐侾俋俆倶俇侽倶俇侽亐侾侽侽侽亖
侾丏俀俆俇
摎偊侾丏俀俆俇
丂

