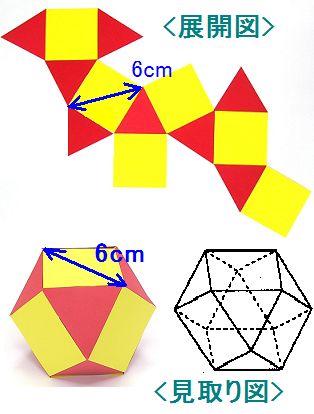
丂嵍忋偺幨恀偼偁傞棫懱偺揥奐恾偱偡丅傑偨嵍壓偼丄揥奐恾傪慻傒棫偰偨偲偒偺棫懱偺尒庢傝恾偱偡丅
丂揥奐恾偱帵偟偨偲偍傝丄偙偺棫懱偼俇枃偺惓曽宍偲俉枃偺惓嶰妏宍偐傜偱偒偨侾係柺懱偱偡丅
丂偨偩偟丄惓曽宍偺懳妏慄偺挿偝偼俇們倣偱偁傝丄惓曽宍偲惓嶰妏宍偺堦曈偺挿偝偼摍偟偄偙偲偑暘偐偭偰偄傑偡丅
丂偙偙偱栤戣偱偡丅偙偺棫懱偺懱愊偼壗cm3偵側傞偱偟傚偆偐丅
丂
丂乮仸幨恀偺傛偆側棫懱傪弨惓懡柺懱偲傛偽傟傑偡丅弨惓懡柺懱偼16庬椶偁傞偦偆偱偡丅偦偟偰丄俆庬椶偺惓懡柺懱偺壗傟偐傪壛岺偡傞偙偲偵傛偭偰摫偔偙偲偑偱偒傞偙偲傪抦傝傑偟偨丅偙偺棫懱傕丄偁傞惓懡柺懱傪壛岺偟偰偱偒傞偼偢偱偡丅乯