「今月の問題」　第９２回　（平成１９年５月）

＜サイコロの目のつけ方の規則性＞

さいころの目のつけ方には次のような規則性があることが分りました。

@　サイコロはどうして表と裏の目をたすと７になる

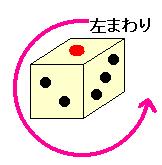
A １，２，３は左まわりの順になる。

（下図）

　上図は１１種類ある立方体の展開図の１つです。
この展開図に左の規則性を使ってサイコロに目を書きます。

ここで、問題です。
この展開図に目を書き込む場合、何通りあるか考えてください。

ただし、（Ａ）と（Ｂ）は回転させると同じになりますから１通りと考えて下さい。

＜正解者一覧表＞　 　　　　　　　　　　　　
正解者順位 　　　　ｎａｍｅ　　　 　　メール到着日時　　 　　備　考　　
　１ 呑ちゃん　さん2007/5/1　0:03最近日記を始めました
　２ゴンとも　さん2007/5/1　0:03豊川市　
　３ダンディ海野　さん2007/5/1　0:14大阪府　
　４なにわ　さん2007/5/1　0:16西宮市　
　５ma-mu-ta　さん2007/5/1　0:16東京都　
　６Walkin' BOA　さん2007/5/1　0:20　
　７エトランゼ　さん2007/5/1　0:31　
　８信三　さん2007/5/1　5:33シリコンバレー　
　９堤真人　さん2007/5/1　6:26大阪府中1　
１０巷の夢　さん2007/5/1　7:07宮城県出身　
１１経友会の進作　さん2007/5/1　8:39京都府木津町68歳
１２uchinyan　さん2007/5/1　10:22東京都　
１３algebra　さん2007/5/1　11:20　
１４fisherman　さん2007/5/1　13:23豊岡市・塾講師　
１５りーくん　さん2007/5/1　13:41埼玉県　
１６NAMPOTのPOT　さん2007/5/1　17:22　
１７teki　さん2007/5/1　23:13大阪府　
１８スモークマン　さん2007/5/2　2:08　
１９いちもく　さん2007/5/2　5:45立川市　
２０akira　さん2007/5/3　6:50東京都　
２１永田竜太郎　さん2007/5/4　18:57元竹中生　
２２ 算数の森　さん2007/5/6　0:31兵庫県、プロ家庭教師
２３ろしなんて　さん2007/5/6　2:01　
２４ 安曇野りんご　さん2007/5/7　9:01只今りんごの花満開
２５プロビーム　さん2007/5/7　13:16岩手県大船渡市
２６kasama　さん2007/5/7　23:50和歌山県プログラマ
２７ banyanyan　さん2007/5/11　7:21京都市
２８ t.yamazaki　さん2007/5/12　18:00神奈川県
２９tomo2　さん2007/5/14　16:09仕事中の息抜き＠東京
３０ujitaka2001　さん2007/5/31　17:17YRP野比在住

答は１２通りでした。次のように回答の書き込みを頂きました。

[72] さいころの置き方 投稿者：なか 投稿日：2007/05/15(Tue) 16:04 [返信]

さいころの置き方と考えてもいいですね。
上面が６通り。側面の回転が４通りで２４通り。
ただし、展開図の点対称を除けといわれているので、
２４÷２＝１２通り。

　
[71] 「表裏の目の和が７」だけなら 投稿者：ダンディ海野 投稿日：2007/05/02(Wed) 18:19 [返信]

サイコロには、１・２・３が左回りのものと右回りのものの２種類のもの考えられますよね。
　そこで条件として、「表裏の目の和は７である。」だけなら（問題の条件が@だけなら）、
この展開図に目を書き込む方法は・・・・・・・・２４通り・・・ですよね？

　
[70] 立体のばらし方で決まる。 投稿者：スモークマン 投稿日：2007/05/02(Wed) 02:06 [返信]

立体図をばらすことを考えると、連続３個なので、
126,136,156,146 と一つの数に４個対応。
同様に、
215,265,235,245
314,324,354,364

4,5,6 から始まるものは、上にでてるものの逆になるだけだから、結局、3*4=12 通り。♪

　
[69] 無題 投稿者：fisherman 投稿日：2007/05/01(Tue) 13:53 [返信]

（1，6）（2，5）（3，4）の組に分ける。右上を中心に（1，6）を固定すると２×２＝４通り考えられる。目の順序が決まっているので（1，6）の入れ替えは考えない。あとは（2，5）（3，4）を固定する場合も同様であるから，４×３＝１２通りである。

　
[68] 要するに 投稿者：uchinyan 投稿日：2007/05/01(Tue) 10:38 [返信]

1 の目を決めると，2 の目の入り方は 1 の目を中心に 4 通り。
3 の目は規則の(2)より，4, 5, 6 の目は規則の(1)より，決まってしまいます。
後は 1 の目の入り方だけですが，対称性より 3 通り。
したがって，4 * 3 = 12 通り。
一応，図も描いて確認しました (^^;

　
[67] 意外と少ない 投稿者：ダンディ海野 投稿日：2007/05/01(Tue) 00:39 [返信]

下段左端の目を決めると、その隣の目は４通り考えられる。
　２つの目を決めるとき、１・２・３が左回りだと決まってい
るので残りの目はすべて自動的に決まってしまう。（１通り）

下段左端の目は６通りあるから、６＊４＝２４（通り）だが
このなかには(A)と(B)のように回転させると同じものが２つ
ずつあるから、２４／２＝１２（通り）