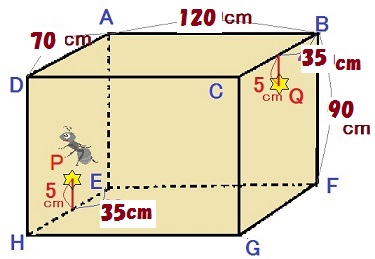
右の図に示すような、縦、横、高さが70cm、120cm、90cmの直方体(ABCD-EFGH)の容器があります。
この直方体の面(BCGF)の辺BCの中央から5cmの下の点Qに蜜がついています。
また、面(ADHE)の辺EHの中央から5cmの上の点Pに蟻がいます。
このとき、蟻が直方体の面の蜜のところまで這っていきます。
ここで問題です。
蟻が這っていくのに最短距離は何cmでしょうか。ただし、蟻は直方体の6面のどの面も歩くことができます。
|
<問題> 右の図に示すような、縦、横、高さが70cm、120cm、90cmの直方体(ABCD-EFGH)の容器があります。 この直方体の面(BCGF)の辺BCの中央から5cmの下の点Qに蜜がついています。 また、面(ADHE)の辺EHの中央から5cmの上の点Pに蟻がいます。 このとき、蟻が直方体の面の蜜のところまで這っていきます。 ここで問題です。 蟻が這っていくのに最短距離は何cmでしょうか。ただし、蟻は直方体の6面のどの面も歩くことができます。 |
 |
<正解者一覧表>
順位
name
メール到着日時
備 考
1
源内シンガポール さん
2016/5/1 0:05
2
algebra さん
2016/5/1 0:06
神奈川県
3
朝霞おじ さん
2016/5/1 0:09
埼玉県
4
kou さん
2016/5/1 0:10
さいたま
5
鯨鯢(Keigei) さん
2016/5/1 0:12
7
Mr.ダンディ さん
2016/5/1 0:12
8
男はつらいよ さん
2016/5/1 0:13
神奈川県
9
AKIRA さん
2016/5/1 0:15
愛知県
10
デアルケ さん
2016/5/1 0:15
三重県紀北町
11
GOGOGIANTS さん
2016/5/1 0:22
12
バニラ さん
2016/5/1 0:24
13
そんなの関係ねえ さん
2016/5/1 0:26
14
川上智弘 さん
2016/5/1 0:27
兵庫県
15
マッキー27 さん
2016/5/1 0:28
愛知県
16
ゴンとも さん
2016/5/1 1:43
豊川市
17
さん
2016/5/1 1:48
18
巷の夢 さん
2016/5/1 7:40
神奈川県在住
19
JUST_COMMUNICATION さん
2016/5/1 9:59
20
NNR4 さん
2016/5/1 10:21
兵庫県
21
uchinyan さん
2016/5/1 11:47
東京都
22
GUTENTAG さん
2016/5/1 16:16
滋賀県
23
次郎長 さん
2016/5/1 17:19
連休ボケ兵庫県
24
いちもく さん
2016/5/1 17:51
立川市
25
寺脇 犬 さん
2016/5/1 18:29
大阪市
26
まいすた さん
2016/5/1 22:22
27
スモークマン さん
2016/5/2 22:00
@新倉敷
28
ユートニウム さん
2016/5/3 5:43
29
石原ゼミ さん
2016/5/3 21:49
30
うさぎとかめ さん
2016/5/4 10:44
31
つねまる さん
2016/5/6 9:34
千葉県
32
やぶコウノトリ さん
2016/5/6 12:17
兵庫県
33
りーくん さん
2016/5/7 22:32
埼玉県
34
コーセージ さん
2016/5/8 0:08
大阪府枚方
35
いぬたこ さん
2016/5/9 17:28
ちば
36
うたねこ さん
2016/5/9 20:16
とうきょう
37
保和 さん
2016/5/10 3:20
愛知
答えは、200cmでした